��Ŀ����
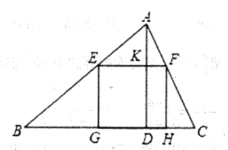
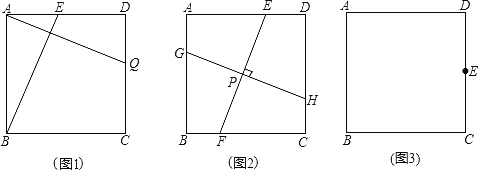
����Ŀ����ϰ����ϣ���ʦ��ͬѧ���Կα�һ��ϰ�⡰��ͼ1��A��B��C��D�ļҹ����ֱ������������γ�����ĸ����ϣ��ֿ�E��Q�ֱ�λ��AD��DC�ϣ���ED��QC��֤������ֱ·BE��AQ��BE��AQ����Ϊ������չ��ѧ̽����
(1)����˼���������������е�ED��QCȥ�����������е�BE��AQ��Ϊ�����������������䣬��ôBE��AQ����������д���𰸲�˵�����ɣ�
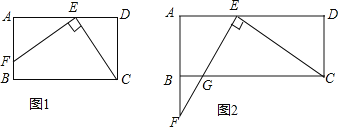
(2)���������������֮��С���ͬѧ�ܴ�����������������ͼ2����������ABCD����һ��P������P��EF��GH����E��F�ֱ��������εĶԱ�AD��BC�ϣ���G��H�ֱ��������εĶԱ�AB��CD�ϣ���ôEF��GH����𣿲�˵�����ɣ�
(3)��չӦ�ã�����ԡ�С���ͬѧ�ܡ����֮��С����������뵽������ͼ2�Ľ��۽���������⣺
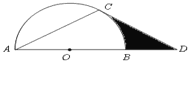
��ͼ3�����߳�Ϊ10cm��������ֽƬABCD�۵���ʹ��A����DC���е�E�����ۺ�ΪMN����N��BC���ϣ���M��AD���ϣ����㻭���ۺۣ����ۺ�MN�ij����� �����߶�DM�ij����� ����
���𰸡�(1)BE��AQ�����ɼ�������(2)EF��GH�����ɼ�������(3)5![]() cm��
cm��![]() m��
m��
��������
��1������BE��AQ�������AEB=��AQD������AB=AD����BAE=��ADQ=90������֤����ABE�ա�DAQ������۵ó���
��2����ͨ����������֪������ص�����������⣮��BM��EF��AD��M����AN��GH��CD��N����ôBM=EF��AN=GH����1����������֤����ABM����DANȫ�ȣ���ôBM=AN����EF=GH��
��3�����AE�����ɣ�2����֪MN=AE����DM=xcm����AM=ME=��10-x��cm��������δ֪��ת����ֱ��������DME�У����ù��ɶ�����ɣ�
(1)BE��AQ��
�������£���BE��AQ��
���AEB��90�㩁��DAQ����AQD��
�֡�AB��AD����BAE����QDA��90�㣬
���ABE�ա�DAF(AAS)��
��BE��AQ��
(2)EF��GH���������£�
��ͼ1����BM��EF��AD��M����AN��GH��CD��N��

��AB��CD��AD��BC��
���ı���AGHN�ı���BMEF����ƽ���ı��Σ�
��BM��EF��AN��GH��
��(1)֪��BM��AN��
��EF��GH��
(3)��ͼ2��
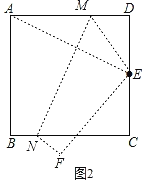
��EΪDC���е㣬
��DE��5cm��
��![]()
��MN��AE����(2)��֪��
��MN��AE��5![]() cm��
cm��
��DM��xcm����AM��ME��(10��x)cm��
��Rt��DME��DM2+DE2��ME2��
��x2+52��(10��x)2��
���x��![]() ��
��
���߶�DM�ij�Ϊ![]() cm��
cm��
�ʴ�Ϊ��5![]() cm��
cm��![]() cm��
cm��

 ������ÿ�ʱ�Ż���ҵϵ�д�
������ÿ�ʱ�Ż���ҵϵ�д�����Ŀ��ijУ���������˵�����ģ�⿼�ԣ���У�쵼Ϊ���˽�ѧ������ѧ����������������鲿��ѧ������ѧ�ɼ����������������ݽ���������������
�����·���������������
�ȼ��ȼ� | ������ | �����ܷ� | ���� |
A | 110��X��120 | P | 4 |
B | 100��X��110 | 843 | n |
C | 90��X��100 | 574 | m |
D | 80��X��90 | 171 | 2 |
�����������������ͳ��ͼ��

��1�����m���� ����n���� ������ѧ�ɼ�����λ�����ڵĵȼ��� ����
��2�������У��1200��ѧ���μ��˱���ģ��⣬����D�ȼ���������
��3����֪��������ѧ������ѧ�ɼ�ƽ����Ϊ102�֣���A�ȼ�ѧ������ѧ�ɼ���ƽ��������