题目内容
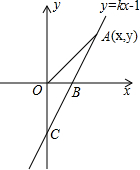 如图,直线y=kx-1与x轴、y轴分别交于B、C两点,tan∠OCB=
如图,直线y=kx-1与x轴、y轴分别交于B、C两点,tan∠OCB=| 1 |
| 2 |
(1)求B点的坐标和k的值;
(2)若点A(x,y)是第一象限内的直线y=kx-1上的一个动点.当点A运动过程中,试写出△AOB的面积S与x的函数关系式;
(3)探索:在(2)的条件下:
①当点A运动到什么位置时,△AOB的面积是
| 1 |
| 4 |
②在①成立的情况下,x轴上是否存在一点P,使△POA是等腰三角形?若存在,请写出满足条件的所有P点的坐标;若不存在,请说明理由.
分析:本题考查一次函数的综合应用,在(1)中需根据OC=1求出B点坐标,再利用待定系数法求出k值;(2)中利用把△AOB的面积表示出来,在根据x与y之间的关系代入整理;(3)代入求值即可,同时在查找等腰三角形的满足P点的坐标时要根据等腰三角形的性质查找.
解答:解:(1)∵y=kx-1与y轴相交于点C,
∴OC=1;
∵tan∠OCB=
=
,
∴OB=
;
∴B点坐标为:(
,0);
把B点坐标为:(
,0)代入y=kx-1得:k=2;
(2)∵S=
•OB•|y|,y=kx-1,
∴S=
×
(2x-1);
∴S=
x-
;
(3)①当S=
时,
x-
=
,
∴x=1,y=2x-1=1;
∴A点坐标为(1,1)时,△AOB的面积为
;
②存在.
满足条件的所有P点坐标为:
P1(1,0),P2(2,0),P3(
,0),P4(-
,0).(12分)
(注:每题只给出一种解法,如有不同解法请参照评分意见给分)
∴OC=1;
∵tan∠OCB=
| 1 |
| 2 |
| OB |
| OC |
∴OB=
| 1 |
| 2 |
∴B点坐标为:(
| 1 |
| 2 |
把B点坐标为:(
| 1 |
| 2 |
(2)∵S=
| 1 |
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 4 |
(3)①当S=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∴x=1,y=2x-1=1;
∴A点坐标为(1,1)时,△AOB的面积为
| 1 |
| 4 |
②存在.
满足条件的所有P点坐标为:
P1(1,0),P2(2,0),P3(
| 2 |
| 2 |
(注:每题只给出一种解法,如有不同解法请参照评分意见给分)
点评:本题是函数与三角形相结合的问题,在图形中渗透运动的观点是中考中经常出现的问题.

练习册系列答案
相关题目
 如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )
如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )| A、3 | ||
B、
| ||
C、
| ||
D、-
|
 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式| 1 |
| 2 |
| A、x<2 |
| B、x>-1 |
| C、x<1或x>2 |
| D、-1<x<2 |
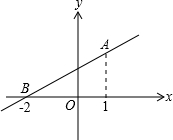 如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为
如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为 7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( )
7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( ) 16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为
16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为