��Ŀ����
����Ŀ����ֱ֪��y=![]() x+3����������ֱ��ཻ��A��B���㣬����P��Q�ֱ����߶�AB��OB�ϵĶ��㣬�ҵ�P����A��B�غϣ���Q����O��B�غϣ�
x+3����������ֱ��ཻ��A��B���㣬����P��Q�ֱ����߶�AB��OB�ϵĶ��㣬�ҵ�P����A��B�غϣ���Q����O��B�غϣ�
��1����OP��AB�ڵ�P����OPQΪ���������Σ���ʱ���������ĵ�Q�м�������ֱ��д����Ӧ��OQ�ij���
��2������P��AB���е�ʱ������OPQ����ABO���ƣ���ʱ���������ĵ�Q�м�������ֱ������Ӧ��OQ�ij���
��3����̽���Ƿ�����Ե�PΪֱ�Ƕ����Rt��OPQ�������ڣ������Ӧ��OQ�ķ�Χ�������OQȡ��Сֵʱ��P�����ꣻ�������ڣ���˵�����ɣ�

���𰸡�(1) ��Q��������OQ�ij�Ϊ2��![]() ��
��![]() ��(2) 2����OQ�ij�Ϊ2��
��(2) 2����OQ�ij�Ϊ2��![]() ��(3)���ڣ�OQȡ��Сֵʱ��P�����꣨
��(3)���ڣ�OQȡ��Сֵʱ��P�����꣨![]() ��
��![]() ����
����
��������
�����������1����ͼ1�У����������ĵ�Q���������������������ۼ�����QO=QP����OP=OQ����PO=PQ��
��2����ͼ2�У����������ĵ�Q��2������![]() ��OB��
��OB��![]() ��
��![]() ��OP��
��OP��![]() ������֤��
������֤��![]() ��
��![]() �����������������������ε����ʼ��ɽ�����⣮
�����������������������ε����ʼ��ɽ�����⣮
��3�����ڣ���OQΪֱ������G������G��AB�����ڵ�Pʱ����OPQ=90�㣬��ʱOQ��ֵ��С���ɴ����OQ�����ɽ�����⣮
�����������1����ͼ1�У����������ĵ�Q��������
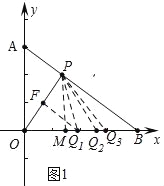
���ɣ���PM��OB��M����OP�Ĵ�ֱƽ���߽�OP��F����OB��![]() ����
����![]() =
=![]() ����
����![]() �ǵ��������Σ���ʱ
�ǵ��������Σ���ʱ![]() =
=![]() OB=2��
OB=2��
��A��0��3����B��4��0����
��OA=3��OB=4��AB=5��
��OP��AB��
��![]() OAOB=
OAOB=![]() ABOP��
ABOP��
��OP=![]() =
=![]() ��
��
��![]() =OPʱ����
=OPʱ����![]() �ǵ��������Σ���ʱ
�ǵ��������Σ���ʱ![]() =
=![]() ��
��
��PO=![]() ʱ����PM��
ʱ����PM��![]() ��
��
��![]() =2OM��
=2OM��
�ߡ�POM=��![]() ����PMO=��OPB��
����PMO=��OPB��
���OPM�ס�OBP��
��![]() =OMOB��
=OMOB��
��OM=![]() ��
��
��![]() =
=![]() .
.
������������OPQΪ����������ʱ�����������ĵ�Q��������OQ�ij�Ϊ2��![]() ��
��![]() ��
��
��2����ͼ2�У����������ĵ�Q��2����
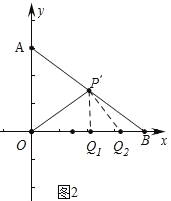
���ɣ���![]() ��OB��
��OB��![]() ��
��![]() ��OP��
��OP��![]() ��
��
��PA=PB����AOB=90�㣬
��PA=PB=PO��
���![]() =��ABO���ߡ�
=��ABO���ߡ�![]() =��AOB��
=��AOB��
���![]() �ס�BAO��
�ס�BAO��
��PA=PB��![]() ��OA��
��OA��
��![]() =
=![]() =
=![]() OB=2��
OB=2��
�ߡ�![]() =��ABO����
=��ABO����![]() =��AOB��
=��AOB��
���![]() �ס�BOA��
�ס�BOA��
��![]() ��
��
��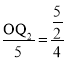 ��
��
��![]() =
=![]() ��
��
������������OPQ����ABO����ʱ�����������ĵ�Q��2����OQ�ij�Ϊ2��![]() ��
��
��3�����ڣ��������£�
��ͼ3�У���OQΪֱ������G������G��AB�����ڵ�Pʱ����OPQ=90�㣬��ʱOQ��ֵ��С��
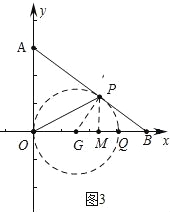
����OG=GP=r��
��AO=AP=3��
��PB=AB=AP=2��
��Rt��PBG�У��ߡ�GPB=90�㣬PG=r��BG=4��r��PB=2��
��![]() ��
��
��r=![]() ��
��
��OQ=2r=3��
����3��OQ��4ʱ����OPQ��Ϊֱ�������Σ�
��PM��OB��M��
��PM��OA��
��![]() ��
��
��![]() ��
��
��PM=![]() ��BM=
��BM=![]() ��
��
��OM=4��![]() =
=![]() ��
��
��OQȡ��Сֵʱ��P�����꣨![]() ��
��![]() ����
����

 �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д� ѧϰʵ����ϵ�д�
ѧϰʵ����ϵ�д�����Ŀ������5�·ݣ�ijУ���꼶ѧ���μ����������п��������ԣ�Ϊ���˽��У���꼶��1����ͬѧ���п������������ȫ��ѧ�����п������ɼ�������ͳ�ƣ����������²�������Ƶ���ֲ����������������ͳ��ͼ����ͼ��������ͼ���е���Ϣ����������⣺
��1����ȫ��ѧ��������m��ֵ��
��2��ֱ��д���ð�ѧ�����п������ɼ�����λ�������ĸ������Σ�
��3���ð��п������ɼ����ֹ���3�ˣ���������2�ˣ�Ů��1�ˣ��������3�������ѡȡ2�˵����꼶���о��齻�������á��б���������״ͼ�������ǡ��ѡ��һ��һŮ�ĸ��ʣ�
���� | �����Σ��֣� | Ƶ�� |
A | 36��x��41 | 2 |
B | 41��x��46 | 5 |
C | 46��x��51 | 15 |
D | 51��x��56 | m |
E | 56��x��61 | 10 |