题目内容
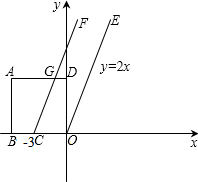
在直角坐标系中,正方形ABOD的边长为5,O为原点,点B在x轴的负半轴上,点D在y轴的正半轴上,直线OE的解析式为y=2x,直线CF过x轴上一点C(-3,0)且与OE平行.现正方形以每秒 的速度匀速沿x轴的正方向平行移动,设
的速度匀速沿x轴的正方向平行移动,设 运动时间为t秒,正方形被夹在直线OE与CF间的部分的面积为S.
运动时间为t秒,正方形被夹在直线OE与CF间的部分的面积为S.
(1)当0≤t<4时,写出S与t的函数关系;
(2)当4≤t≤5时,写出S与t的函数关系,在这个范围内S有无最大值?若有,请求出这个最大值;若没有,请说明理由.
 解:(1)当0≤t<4时,设经过t秒后正方形移动到A1B1MN的位置,如图1,
解:(1)当0≤t<4时,设经过t秒后正方形移动到A1B1MN的位置,如图1,∴OM=
 ,
,当t=4时,BB1=OM=2,
∴点B1在C的左侧,
∴夹在两平行线间的部分是多边形COQNG,
其面积为:平行四边形COPG-△NPQ的面积,
易得平行四边形COPG的面积=15,
又因为点P的纵坐标为5,所以P(
 ,5),
,5),所以:NP=
 -
- ,
,由y=2x知,NQ=2NP,
∴△NPQ面积=
 ,
,∴S=15-
 ,
,
(2)当4≤t≤5时,正方形移动到如图位置,如图2,
当4≤t≤5时,2≤BB1≤2.5,点B1在C、O之间,
∴夹在两平行线间的部分是多边形B1OQNGR其面积为:
平行四边形COPG-△NPQ的面积-△CB1R的面积,
∴S=
 ,
,=
 ,
,所以:当t=
 时,S有最大值为
时,S有最大值为 .
.分析:(1)当0≤t<4时,设经过t秒后正方形移动到A1B1MN的位置如图1,则OM=
 ,当t=4时,BB1=OM=2,则点B1在C的左侧.所以夹在两平行线间的部分是多边形COQNG.
,当t=4时,BB1=OM=2,则点B1在C的左侧.所以夹在两平行线间的部分是多边形COQNG.其面积=平行四边形COPG-△NPQ的面积,易得平行四边形COPG的面积.由点P的纵坐标为5,求得点P.从而求得NP,由y=2x知,NQ=2NP,即求得△NPQ面积.
(2)当4≤t≤5时,正方形移动到如图位置,当4≤t≤5时,2≤BB1≤2.5,点B1在C、O之间,所以夹在两平行线间的部分是多边形B1OQNGR其面积=平行四边形COPG-△NPQ的面积-△CB1R的面积,从而求得.
点评:本题主要考查了二次函数的综合应用,根据二次函数得出相关点的坐标和对称轴的解析式是解题的基础.

练习册系列答案
相关题目

 运动时间为t秒,正方形被夹在直线OE与CF间的部分的面积为S.
运动时间为t秒,正方形被夹在直线OE与CF间的部分的面积为S. (2010•本溪一模)在直角坐标系中,放置一个如图的直角三角形纸片AOB,已知OA=2,∠AOB=30°,D、E两点同时从原点O出发,D点以每秒
(2010•本溪一模)在直角坐标系中,放置一个如图的直角三角形纸片AOB,已知OA=2,∠AOB=30°,D、E两点同时从原点O出发,D点以每秒 (2013•恩施州)如图所示,在直角坐标系中放置一个边长为1的正方形ABCD,将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成的面积为( )
(2013•恩施州)如图所示,在直角坐标系中放置一个边长为1的正方形ABCD,将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成的面积为( )