题目内容
在直角坐标系中，O是坐标原点，正方形OABC的顶点A恰好落在双曲线y=
| ||
| x |
分析：如图，过A作AE⊥OE于E，设A的坐标为（x，y），那么AE=y，OE=x，而A恰好落在双曲线y=
（x＞0）上，由此可以得到xy=
，又OA与x轴正方向的夹角为30°，由此得到x=
y，利用这些关系即可求出x的值，也就可以求出正方形的面积．
| ||
| x |
| 3 |
| 3 |
解答：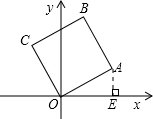
解：如图，过A作AE⊥OE于E，
设A的坐标为（x，y），（x＞0，y＞0）
∴AE=y，OE=x，
而A恰好落在双曲线y=
（x＞0）上，
∴xy=
，
又OA与x轴正方向的夹角为30°，
∴x=
y，
∴
y2=
，
∴y=1，x=
，
∴OA=2，
∴正方形OABC的面积为4．
故答案为4．
解：如图，过A作AE⊥OE于E，设A的坐标为（x，y），（x＞0，y＞0）
∴AE=y，OE=x，
而A恰好落在双曲线y=
| ||
| x |
∴xy=
| 3 |
又OA与x轴正方向的夹角为30°，
∴x=
| 3 |
∴
| 3 |
| 3 |
∴y=1，x=
| 3 |
∴OA=2，
∴正方形OABC的面积为4．
故答案为4．
点评：此题分别考查了反比例函数的图象和性质、正方形的性质及特殊直角三角形的性质，综合性比较强，一起学生熟练掌握相关基础知识才能很好解决这类问题．
练习册系列答案
相关题目
在直角坐标系中，O是坐标原点，点A（3，-2）在一次函数y=-2x+4图象上，图象与y轴的交点为B，那么△AOB面积为
9、如图，在直角坐标系中，O是原点，A在x轴上，B在y轴上，点O的坐标是
20、如图，在直角坐标系中，AC是Rt△OAB的角平分线，点C到AB的距离是5，则点C的坐标是
如图，在直角坐标系中，△AOB是等边三角形，若B点的坐标是（2，0），则A点的坐标是（ ）
如图在直角坐标系中，△AOB是等边三角形，若B点的坐标是（2，0），则A点的坐标是（ ）