��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���![]() ��ͼ����y��������ύ�ڵ�A����x�ύ�ڵ�
��ͼ����y��������ύ�ڵ�A����x�ύ�ڵ�![]() ��
��![]() �����Ϊ
�����Ϊ![]() ����P�ӵ�B��������ÿ��1����λ���ȵ��ٶ�������BO���˶�������Q��O��������x������������Pͬʱ����ͬ���ٶ��˶�����P��
����P�ӵ�B��������ÿ��1����λ���ȵ��ٶ�������BO���˶�������Q��O��������x������������Pͬʱ����ͬ���ٶ��˶�����P��![]() �ύֱ��AB��M��
�ύֱ��AB��M��
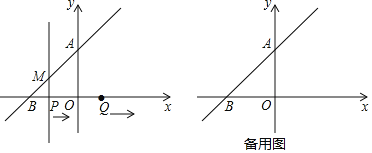
![]() ��ֱ��AB�Ľ���ʽ��
��ֱ��AB�Ľ���ʽ��
![]() ����P���߶�OB���˶�ʱ����
����P���߶�OB���˶�ʱ����![]() �����ΪS����P�˶���ʱ��Ϊt�룬��S��t�ĺ�����ϵʽ
�����ΪS����P�˶���ʱ��Ϊt�룬��S��t�ĺ�����ϵʽ![]() ֱ��д���Ա�����ȡֵ��Χ
ֱ��д���Ա�����ȡֵ��Χ![]() ��
��
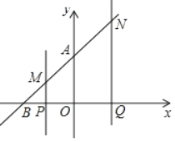
![]() ����Q��
����Q��![]() �ύֱ��AB��N�����˶�������
�ύֱ��AB��N�����˶�������![]() ����B�غ�
����B�غ�![]() ���Ƿ����ijһʱ��
���Ƿ����ijһʱ��![]() ��
��![]() ��ʹ
��ʹ![]() �ǵ��������Σ������ڣ����ʱ��tֵ��
�ǵ��������Σ������ڣ����ʱ��tֵ��
���𰸡�(1)y��x+2��(2)S��t(0��t��2)��(3)���ڣ�t��2��2![]() ��2��
��2��
��������
��1��S��ABO=![]() ��OA��OB=
��OA��OB=![]() ��AO��2=2����OA=2������A��0��2����������⣻
��AO��2=2����OA=2������A��0��2����������⣻
��2��t��ʱ����P������Ϊ��-2+t��0������MP=BP=t��S=![]() ��PQ��MP��������⣻
��PQ��MP��������⣻
��3����MN=MQ��MN=NQ��MQ=NQ�����������⼴�ɣ�
(1)S��ABO��![]() ��OA��OB��
��OA��OB��![]() ��AO��2��2����OA��2������A(0��2)��
��AO��2��2����OA��2������A(0��2)��
����A��B���������һ�κ�������ʽ��y��km+n���ã�![]() ��
��
��ã�![]() ��
��
��ֱ��AB�ı���ʽΪ��y��x+2��
(2)t��ʱ����P������Ϊ(��2+t��0)����MP��BP��t��
S��![]() ��PQ��MP��
��PQ��MP��![]() ��2t��t(0��t��2)��
��2t��t(0��t��2)��
(3)���ڣ����ɣ�
t��ʱ����M��N��Q������ֱ�Ϊ(��2+t��t)��(t��t+2)��(t��0)��
��MN2��4+4��8��MQ2��4+t2��NQ2��(t+2)2��
��MN��MQʱ������8��4+t2��t��2(��ֵ����ȥ)��
��MN��NQʱ��ͬ���ɵã�t��2![]() ��2(��ֵ����ȥ)��
��2(��ֵ����ȥ)��
��MQ��NQʱ��ͬ���ɵã�t��0(��ȥ)��
�ʣ�����MNQ�ǵ���������ʱ��t��2��2![]() ��2��
��2��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�