题目内容
【题目】已知△ABC中,AB=4,BC=5,AC的长是一元二次方程x2﹣15x+54=0的一个根.
(1)求AC的长;
(2)在AC上找一点D,连接BD,使△ABD∽△ACB;
(3)以AC为一边作一个三角形ACM,求出sin∠AMC的值.(所作三角形自己设计)
【答案】(1)AC=6;(2)见解析;当AD=![]() 时,△ABD∽△ACB;(3)sin∠AMC=
时,△ABD∽△ACB;(3)sin∠AMC=![]() .
.
【解析】
(1)解一元二次方程x2-15x+54=0,可得x1=6,x2=9,再根据三角形的三边关系,即可得到AC的范围,进而得出AC的长;
(2)依据相似三角形的对应边成比例,即可得到AD的长,即可得出点D的位置;
(3)以AC为一边作一个等边三角形ACM,即可得到sin∠AMC的值,答案不唯一.
(1)解一元二次方程x2﹣15x+54=0,可得
x1=6,x2=9,
∵5﹣4<AC<5+4,
∴1<AC<9,
∵AC的长是一元二次方程x2﹣15x+54=0的一个根,
∴AC=6;
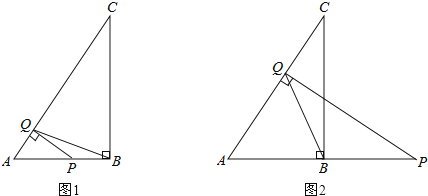
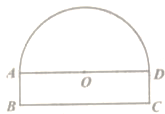
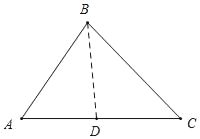
(2)如图所示,当△ABD∽△ACB时,
![]() =
=![]() ,即AB2=AD×AC,
,即AB2=AD×AC,
∴16=AD×6,
∴AD=![]() ,
,
∴当AD=![]() 时,△ABD∽△ACB;
时,△ABD∽△ACB;
(3)如图所示,以AC为一边作一个等边三角形ACM,则∠AMC=60°,
∴sin∠AMC=sin60°=![]() .
.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目