题目内容
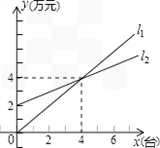
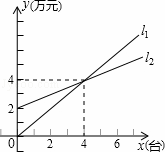
 如图,l1表示某商场一天的电脑销售额与销售量的关系,l2表示该商场一天的销售成本与电脑销售的关系:
如图,l1表示某商场一天的电脑销售额与销售量的关系,l2表示该商场一天的销售成本与电脑销售的关系:(1)一天销售
3
3
台时,销售额等于销售成本;(2)求l1对应的函数表达式,并求当x=6时,销售额是多少万元;
(3)写出利润(销售额-成本)与销售量之间的函数表达式,并求当x=6时,利润是多少万元.
分析:(1)观察图形,当两直线相交时,销售额等于销售成本;
(2)l1过原点,设l1对应的函数关系式为y1=kx,将点(3,4)代入求k的值,再将x=6代入,求销售额;
(3)设l2对应的函数关系式为y2=ax+b,利用“两点法”求直线l2的解析式,再由利润=销售额-成本,求出利润与销售量之间的函数表达式,利用所求函数关系式求利润.
(2)l1过原点,设l1对应的函数关系式为y1=kx,将点(3,4)代入求k的值,再将x=6代入,求销售额;
(3)设l2对应的函数关系式为y2=ax+b,利用“两点法”求直线l2的解析式,再由利润=销售额-成本,求出利润与销售量之间的函数表达式,利用所求函数关系式求利润.
解答:解:(1)由图象可知,当一天销售3台时,销售额等于销售成本.
故答案为:3;
(2)设l1对应的函数关系式为y1=kx,将点(3,4)代入,
得3k=4,解得k=
,
所以,y1=
x;
当x=6时,y1=
×6=8,
即当x=6时,销售额是8万元;
(3)设利润为w(万元),l2对应的函数关系式为y2=ax+b,
把点(0,2),(3,4)代入,得
,
解得
,
所以,y2=
x+2,
则w=y1-y2=
x-(
x+2)=
x-2,
当x=6时,w=
x-2=
×6-2=2(万元),
即:当x=6时,利润是2万元.
故答案为:3;
(2)设l1对应的函数关系式为y1=kx,将点(3,4)代入,
得3k=4,解得k=
| 4 |
| 3 |
所以,y1=
| 4 |
| 3 |
当x=6时,y1=
| 4 |
| 3 |
即当x=6时,销售额是8万元;
(3)设利润为w(万元),l2对应的函数关系式为y2=ax+b,
把点(0,2),(3,4)代入,得
|
解得
|
所以,y2=
| 2 |
| 3 |
则w=y1-y2=
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
当x=6时,w=
| 2 |
| 3 |
| 2 |
| 3 |
即:当x=6时,利润是2万元.
点评:本题考查了一次函数的应用.关键是根据图象,求出两直线的解析式.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
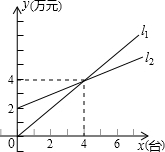 如图,l1表示某商场一天的手提电脑销售额与销售量的关系,l2表示该商场一天的销售成本与手提电脑销售量的关系.
如图,l1表示某商场一天的手提电脑销售额与销售量的关系,l2表示该商场一天的销售成本与手提电脑销售量的关系.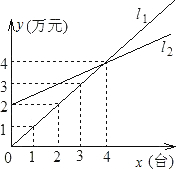 如图,l1表示某商场一天的手提电脑销售额与销售量的关系,l2表示该商场一天的销售成本与手提电脑销售量的关系:
如图,l1表示某商场一天的手提电脑销售额与销售量的关系,l2表示该商场一天的销售成本与手提电脑销售量的关系: