题目内容
【题目】如图,在△ABC中,∠ABC的平分线BF与△ABC的外角平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E。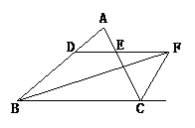
(1)写出图中所有的等腰三角形,并选择其中一个说明理由。
(2)直接写出BD,CE,DE之间的数量关系。
(3)若DE=5cm,CE=8cm,BF=24cm,求△BDF的面积。
【答案】
(1)解:△DBF、△ECF
以说明△DBF为例:
∵BF平分∠ABC
∴∠DBF=∠CBF
∵DF∥BC
∴∠CBF=∠DFB
∴∠DBF=∠DFB,即△DBF为等腰三角形。
(2)解:BD=DE+CE
理由如下:
因为△DBF、△ECF为等腰三角形
BD=FD,CE=EF
DF=DE+EF=DE+CE
所以BD=DE+CE
(3)解: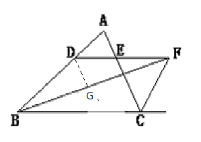
如图,做DG⊥BF与G
∵BD=FD
∴FG=![]() BF=12cm
BF=12cm
又DF=DE+CE=5+8=13cm
由勾股定理得DG=5cm
S△BDF=![]() BF×DG=
BF×DG=![]() ×24×5=60cm
×24×5=60cm
答:△BDF的面积为60cm。
【解析】(1)由角平分线加平行线易得等腰三角形,所以由图易得△DBF、△ECF为等腰三角形。
(2)由等腰三角形的性质,利用等量代换易得BD=DE+CE
(3)作BF边上的高,由勾股定理得到高为5。计算得到△BDF的面积为60。

练习册系列答案
相关题目
【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
| -1 | 0 | 1 | 3 |
| -3 | 1 | 3 | 1 |
下列结论:①抛物线的开口向下;②其图象的对称轴为![]() ;③当
;③当![]() 时,函数值
时,函数值![]() 随
随![]() 的增大而增大;④方程
的增大而增大;④方程![]() 有一个根大于4.其中正确的结论有( )
有一个根大于4.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个