题目内容
【题目】(本小题满分14分)
如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(-4,0)、B(0,3),抛物线y=-x2+2x+1与y轴交于点C.
(1)求直线y=kx+b的解析式;
(2)若点P(x,y)是抛物线y=-x2+2x+1上的任意一点,设点P到直线AB的距离为d,求d关于x的函数解析式,并求d取最小值时点P的坐标;
(3)若点E在抛物线y=-x2+2x+1的对称轴上移动,点F在直线AB上移动,求CE+EF的最小值. 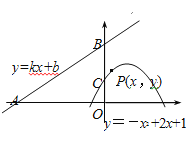
【答案】(1) y=![]() x+3;(2)P(
x+3;(2)P(![]() ,
,![]() );(3)
);(3)![]() .
.
【解析】
试题分析:(1)将A、B两点坐标代入y=kx+b中,求出k、b的值;(2)作出点P到直线AB的距离后,由于∠AHC=90°,考虑构造“K形”相似,得到△MAH、△OBA、△NHP三个三角形两两相似,三边之比都是3∶4∶5.由“![]() ”可得
”可得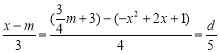 ,整理可得d关于x的二次函数,配方可求出d的最小值;(3)如果点C关于直线x=1的对称点C′,根据对称性可知,CE=C′E.当C′F⊥AB时,CE+EF最小.
,整理可得d关于x的二次函数,配方可求出d的最小值;(3)如果点C关于直线x=1的对称点C′,根据对称性可知,CE=C′E.当C′F⊥AB时,CE+EF最小.
试题解析:
解:(1)∵y=kx+b经过A(-4,0)、B(0,3),
∴![]() ,解得k=
,解得k=![]() ,b=3.
,b=3.
∴y=![]() x+3.
x+3.
(2)过点P作PH⊥AB于点H,过点H作x轴的平行线MN,分别过点A、P作MN的垂线段,垂足分别为M、N.
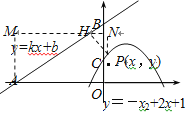
设H(m,![]() m+3),则M(-4,
m+3),则M(-4,![]() m+3),N(x,
m+3),N(x,![]() m+3),P(x,-x2+2x+1).
m+3),P(x,-x2+2x+1).
∵PH⊥AB,∴∠CHN+∠AHM=90°,∵AM⊥MN,∴∠MAH+∠AHM=90°.
∴∠MAH=∠CHN,∵∠AMH=∠CNH=90°,∴△AMH∽△HNP.
∵MA∥y轴,∴△MAH∽△OBA.∴△OBA∽△NHP.
∴![]() .
.
∴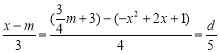 .
.
整理得:![]() ,所以当x=
,所以当x=![]() ,即P(
,即P(![]() ,
,![]() ).
).
(3)作点C关于直线x=1的对称点C′,过点C′作C′F⊥AB于F.过点F作JK∥x轴,,分别过点A、C′作J⊥JK于点J,C′K⊥JK于点K.则C′(2,1)
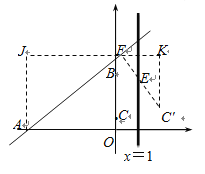
设F(m,![]() m+3)
m+3)
∵C′F⊥AB,∠AFJ+∠C′FK=90°,∵CK⊥JK,∴∠C′+∠C′FK=90°.
∴∠C′=∠AFJ,∵∠J=∠K=90°,∴△AFJ∽△FC′K.
∴![]() ,∴
,∴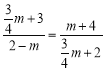 ,解得m=
,解得m=![]() 或-4(不符合题意).
或-4(不符合题意).
∴F(![]() ,
,![]() ),∵C′(2,1),∴FC′=
),∵C′(2,1),∴FC′=![]() .
.
∴CE+EF的最小值=C′E=![]() .
.

【题目】为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图:
甲、乙射击成绩统计表
平均数 | 中位数 | 方差 | 命中10环的次数 | |
甲 | 7 | 4 | 0 | |
乙 | 5.4 | 1 |
甲、乙射击成绩折线图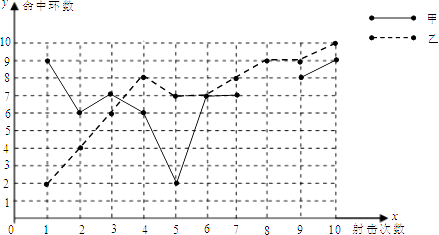
(1)请计算出甲选手第8次命中的环数;
(2)补全上述图表(请直接在表中填空和补全折线图);
(3)你会选择哪位选手参加比赛?说说你的理由.