��Ŀ����
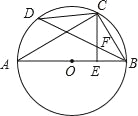
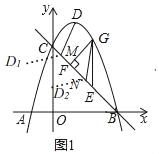
����Ŀ����ͼ1����֪������y����x2+2x+3��x�ύ��A��B���㣬��y�ύ�ڵ�C������ΪD������BC
��1����G��ֱ��BC�Ϸ���������һ���㣨����B��C�غϣ�������G��y���ƽ���߽�ֱ��BC�ڵ�E����GF��BC�ڵ�F����M��N���߶�BC���������㣬��MN��EF������DM��GN������GEF���ܳ����ʱ����DM+MN+NG����Сֵ��
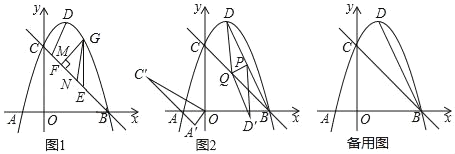
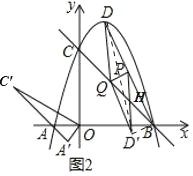
��2����ͼ2������BD����P���߶�BD���е㣬��Q���߶�BC��һ���㣬����DQ������DPQ��PQ���ۣ����߶�D��P���е�ǡ�������߶�BQ�ϣ�����AOC�Ƶ�O��ʱ����ת60��õ���A��OC�䣬��TΪ����ƽ����һ�㣬���Ե�Q��A�䡢C�䡢TΪ������ı�����ƽ���ı���ʱ�����T�����꣮
���𰸡���1��DM+MN+NG��СֵΪ![]() ����2����T������Ϊ��
����2����T��������![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��������
��1���������B��C��D�����꣬����ֱ��BC����ʽ�ҵõ���OCB��45������GE��y���GF��BC�ɵ���GEF�ǵ���ֱ�������Σ���GE���ʱ���ܳ�������G����Ϊ��a����a2+2a+3�������E��a����a+3�������е�GE��a�ĺ�����ϵʽ���䷽����������ֵ���õ���ʱ��G�����EF�ij������õ�MN������DM+MN+NG��Сֵת��Ϊ��DM+NG��Сֵ������D����ֱ��BC�ĶԳƵ�D1����ͨ��ƽ��MD1��D2�������������������Ļ���ͼ����⣮
��2���ɷ��۵�DD'��PQ��PD��PD'������PΪBD�е�֤����BD'D��90������PQ��BD'����D'P�е�H��BQ�ϣ���֤��PQH�ա�D'BH��������D'Q��BP���ı���DQD'PΪ���Σ���DQ��DP����Q������Ϊ��q����q+3�������з�����ã��ٸ�������ѵ�A'��C'������Ե�Q��A����C����TΪ������ı�����ƽ���ı��Σ�Ҫ���з������ۣ����ͼ�Σ�����ƽ���ı��ζԱ�ƽ�е����ʣ���ƽ������ķ���������õ�T��
��1��y����x2+2x+3������x��3����x+1��������x��1��2+4
����������x�ύ�ڵ�A����1��0������B��3��0������y�ύ�ڵ�C��0��3��������D��1��4����
��ֱ��CB����ʽ��y����x+3����BCO��45��
��GE��y�ᣬGF��BC
���GEF����BCO��45������GFE��90��
���GEF�ǵ���ֱ�������Σ�![]() ��
��
��C��GEF��EF+FG+GE����![]() +1��GE
+1��GE
���G��a����a2+2a+3�������E��a����a+3��������0��a��3
��GE����a2+2a+3������a+3������a2+3a![]()
��a![]() ʱ��GE�����ֵΪ
ʱ��GE�����ֵΪ![]() ��
��
���GEF���ܳ����ʱ�� ![]()
��![]() E��ɿ�����F����ƽ��
E��ɿ�����F����ƽ��![]() ����λ������ƽ��
����λ������ƽ��![]() ����λ
����λ
��ͼ1������D����ֱ��BC�ĶԳƵ�D1����1��2������N��ND2��D1M��ND2��D1M
��DM��D1M��ND2�� ![]() ,��
,��![]()
��DM+MN+NG��MN+ND2+NG
����D2��N��G��ͬһֱ����ʱ��ND2+NG��D2GΪ��Сֵ
��
��DM+MN+NG��СֵΪ![]()
��2������DD'��D'B����D'P��BQ����ΪH����ͼ2��
�ߡ���DPQ��PQ���۵���D'PQ
��DD'��PQ��PD��PD'��DQ��D'Q����DQP����D'QP
��PΪBD�е�
��PB��PD��PD'��P��2��2��
���BDD'��ֱ�������Σ���BD'D��90��
��PQ��BD'
���PQH����D'BH
��HΪD'P�е�
��PH��D'H
����PQH����D'BH��
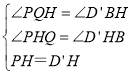
���PQH�ա�D'BH��AAS��
��PQ��BD'
���ı���BPQD'��ƽ���ı���
��D'Q��BP
���DPQ����D'QP
���DQP����DPQ
��DQ��DP
��DQ2��DP2����2��1��2+��2��4��2��5
��Q��q����q+3����0��q��3��
����q��1��2+����q+3��4��2��5
��ã�![]() ����ȥ��
����ȥ��
����Q����Ϊ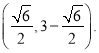
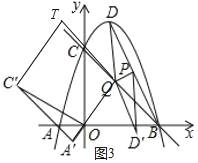
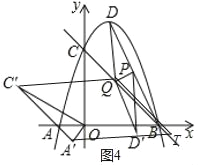
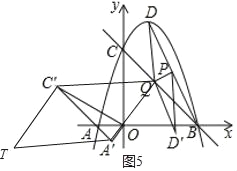
�ߡ�AOC�Ƶ�O��ʱ����ת60���õ���A��OC��
��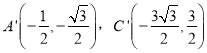
��A'��C'�������Ϊ![]() ���������Ϊ
���������Ϊ![]()
A'��Q�������Ϊ![]() ���������Ϊ
���������Ϊ![]()
����ƽ���ı���A'C'TQʱ����ͼ3������T������Ϊ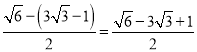 ��������Ϊ
��������Ϊ![]()
����ƽ���ı���A'C'QTʱ����ͼ4������T������Ϊ![]() ��������Ϊ
��������Ϊ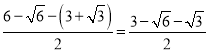
����ƽ���ı���A'TC'Qʱ����ͼ5������T������Ϊ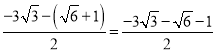 ��������Ϊ
��������Ϊ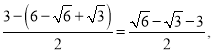
������������T��������![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ��
��

 �ظ���ʦ�㲦ϵ�д�
�ظ���ʦ�㲦ϵ�д� �ľ�ͼ���ʱ�ȷ�ϵ�д�
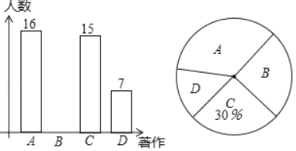
�ľ�ͼ���ʱ�ȷ�ϵ�д�����Ŀ��ij������������ÿ̨���۷ֱ�Ϊ2000Ԫ��1700Ԫ��A��B�����ͺŵĿյ�������ǽ����ܵ����������
����ʱ�� | �������� | �������� | |
A���ͺ� | B���ͺ� | ||
��һ�� | 3̨ | 5̨ | 18000Ԫ |
�ڶ��� | 4̨ | 10̨ | 31000Ԫ |
�����ۡ��ۼ۾����ֲ��䣬������������������ɱ���
��1����A��B�����ͺŵĿյ������۵��ۣ�
��2�����������ò�����54000Ԫ�Ľ���ٲɹ��������ͺŵĿյ���30̨����A���ͺŵĿյ�����ܲɹ�����̨��