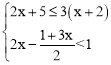��Ŀ����
����Ŀ����ij�ź���ͼ���������������۲�����������ͼ��O��0��0����B��6��0����C��6��8�����������۲��ȷ����Բ�������Ǻ������ﱣ������
��1��ijʱ�̺����ϳ���һ�洬A���ڹ۲��O���Aλ�ڱ�ƫ��45�㣬ͬʱ�ڹ۲��B���Aλ�ڱ�ƫ��30�㣬��۲��B��A���ľ��룮��![]() ��
��
��2�����洬A�ɣ�1����λ�����������������Ƿ����뺣�����ﱣ������ͨ������ش���
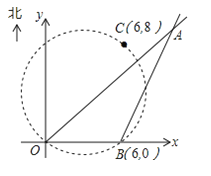
���𰸡���1��16.2����2������
��������
��1������A��AD��![]() ���ڵ�D�������⣬�á�BAD=30������Rt��ABD�У���BD=
���ڵ�D�������⣬�á�BAD=30������Rt��ABD�У���BD=![]() ����AB=2
����AB=2![]() ���ɹ��ɶ����ã�AD=
���ɹ��ɶ����ã�AD= ![]() ������ͼ�εõ�OD=OB+BD=6+x����AB=2x=6(
������ͼ�εõ�OD=OB+BD=6+x����AB=2x=6(![]() )��16.2
)��16.2
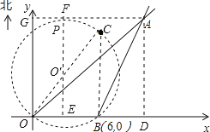
��2������A��AG��y���ڵ�G������O����O��E��OB�ڵ�E�����ӳ�EO�佻AG�ڵ�F���ɴ��������ã�OE=BE=3����Rt��OO��E�У��ɹ��ɶ����ã�O��E=4������O��F=5+3![]() >5.
>5.
��1������A��AD��![]() ���ڵ�D�������⣬�á�BAD=30������Rt��ABD�У���BD=
���ڵ�D�������⣬�á�BAD=30������Rt��ABD�У���BD=![]() ����AB=2
����AB=2![]() ���ɹ��ɶ����ã�AD=
���ɹ��ɶ����ã�AD= ![]() ��������֪��OD=OB+BD=6+
��������֪��OD=OB+BD=6+![]() ����Rt��AOD�У�OD=AD��6+
����Rt��AOD��OD=AD��6+![]() =
=![]()
��![]() =3��
=3��![]() +1����
+1����
��AB=2![]() =6��
=6��![]() +1����16.2
+1����16.2
�����۲��B��A���ľ���Ϊ16.2��
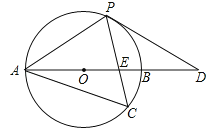
��2������CB��CO����CB��y�ᣬ���CBO=90������O��Ϊ��O��B��C������ȷ��Բ��Բ�ģ�
��OCΪ��O����ֱ����
����֪��OB=6��CB=8���ɹ��ɶ�����OC=![]()
��뾶OO��=5
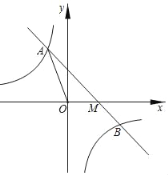
����A��AG��y���ڵ�G��
����O����O��E��OB�ڵ�E�����ӳ�EO����AG�ڵ�F��
�ɴ��������ã�OE=BE=3������Rt��OO��E�У��ɹ��ɶ����ã�O��E=4
���ı���FEDAΪ���Σ���EF=DA����AD=![]() =9+3
=9+3![]()
��O��F=9+3![]() -4=5+3
-4=5+3![]()
��5+3![]() ��5����O��F��r
��5����O��F��r
��ֱ��AG���O�����룬A��������뺣�����ﱣ������

����Ŀ���ס�����λͬѧ5����ѧѡ�����ijɼ�ͳ�����±�������5�ο��Ե��ܳɼ���ͬ����ͬѧ������������⣺
��1 �� | ��2 �� | �� 3�� | �� 4�� | ��5 �� | |
�׳ɼ� | 90 | 40 | 70 | 40 | 60 |
�ҳɼ� | 70 | 50 | 70 |
| 70 |
��1��ͳ�Ʊ��У���![]() ��ֵ����ͬѧ�ɼ��ļ���Ϊ���٣�
��ֵ����ͬѧ�ɼ��ļ���Ϊ���٣�
��2��Сӱ�����˼�ͬѧ�ijɼ�ƽ����Ϊ60��������![]() [(90��60)2+(40��60)2+(70��60)2+(40��60)2+(60��60)2]��360.
[(90��60)2+(40��60)2+(70��60)2+(40��60)2+(60��60)2]��360.
���������ͬѧ�ɼ���ƽ�����ͷ��
��3����ƽ�����ͷ���ĽǶȷ�����������λͬѧ˭�ijɼ����ȶ�.
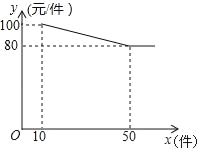
����Ŀ��С���ֻ�Խ��Խ�ܵ����ڵ�ϲ�������ֿ�ʽ���Ͷ���г���ij�꾭Ӫ��A���ֻ�ȥ�������ܶ�Ϊ50000Ԫ������ÿ�����ۼ۱�ȥ�꽵��400Ԫ����������������ͬ�������ܶ��ȥ�����20%��
��1������A���ֻ�ÿ���ۼ۶���Ԫ��
��2���õ�ƻ��½�һ��A���ֻ���B���ֻ���60������B���ֻ��Ľ�������������A���ֻ�������������Ӧ��ν�������ʹ�����ֻ�������ࣿA��B�����ֻ��Ľ��������ۼ۸����±���
A���ֻ� | B���ֻ� | |
�����۸�Ԫ�� | 1100 | 1400 |
���ۼ۸�Ԫ�� | ��������ۼ۸� | 2000 |