题目内容
方程 （X-1）·(X2+17X-3)="0" 的三根分别为X1 ,X2 ,X3 .则X1 X2 + X2 X3 + X1X3 =（ ）
| A． 14 | B． 13 | C．－14 | D．－20 |
D
分析：根据方程（x-1）?（x2+17x-3）=0易求出方程的一根为1，令x1=1，令x2+17x-3=0的两根为x2，x3，根据根与系数的关系，即可求出两根之积和两根之和，再将x1x2+x2x3+x1x3变形为两根之积和两根之和的形式解答即可．
解答：解：∵（x-1）?（x2+17x-3）=0，
∴令x1=1，令x2+17x-3=0的两根为x2，x3，
则x2+x3=-17，x2?x3=-3，
故x1x2+x2x3+x1x3=x1（x2+x3）+x2x3=-17+（-3）=-20．
故选D．
解答：解：∵（x-1）?（x2+17x-3）=0，
∴令x1=1，令x2+17x-3=0的两根为x2，x3，
则x2+x3=-17，x2?x3=-3，
故x1x2+x2x3+x1x3=x1（x2+x3）+x2x3=-17+（-3）=-20．
故选D．
练习册系列答案
相关题目
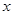的一元二次方程
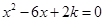有两个不相等的实数根，则实数
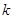的取值范围是 （ ）
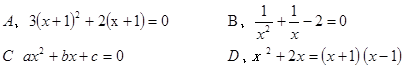
元/
，预计2013年将达到
元/
，根据题意，所列方程为
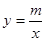的
有两个不相等的实数根，则
的取值范围是 ____▲____
，根据题意所列方程为（ ）
