题目内容
 已知:如图,四边形ABCD是平行四边形,延长BC到E,使AE=AB,连接AC、DE.
已知:如图,四边形ABCD是平行四边形,延长BC到E,使AE=AB,连接AC、DE.
(1)写出图中三对你认为全等的三角形(不再添加其他字母和辅助线);
(2)选择你在(1)中写出的任意一对全等三角形进行证明.
解:(1)①△ABC≌△CDA;②△ACE≌△DEC;③△CAD≌△EDA;④△ABC≌△EAD.…(3分)
(2)证明:△ABC≌△CDA. …(4分)
∵四边形ABCD是平行四边形,
∴AD=BC,∠DAC=∠BCA.…(6分)
又∵AC=CA(公共边),
∴△ABC≌△CDA(SAS).…(9分)
分析:(1)根据全等三角形的判定定理写出图中的全等三角形;
(2)证明:△ABC≌△CDA.根据平行四边形的对边相等、对角线平分对角的性质可以推知AD=BC,∠DAC=∠BCA;然后由全等三角形的判定定理SAS证得△ABC≌△CDA.
点评:本题考查了平行四边形的性质、全等三角形的判定.解题时,(1)应注意做到不重不漏,(2)应结合图形善于运用分析法按照位置关系找出证明全等三角形的三个条件,并注意隐含条件(如本题中的AC=CA).
(2)证明:△ABC≌△CDA. …(4分)
∵四边形ABCD是平行四边形,
∴AD=BC,∠DAC=∠BCA.…(6分)
又∵AC=CA(公共边),
∴△ABC≌△CDA(SAS).…(9分)
分析:(1)根据全等三角形的判定定理写出图中的全等三角形;
(2)证明:△ABC≌△CDA.根据平行四边形的对边相等、对角线平分对角的性质可以推知AD=BC,∠DAC=∠BCA;然后由全等三角形的判定定理SAS证得△ABC≌△CDA.
点评:本题考查了平行四边形的性质、全等三角形的判定.解题时,(1)应注意做到不重不漏,(2)应结合图形善于运用分析法按照位置关系找出证明全等三角形的三个条件,并注意隐含条件(如本题中的AC=CA).

练习册系列答案
相关题目
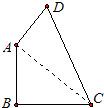 已知,如图,四边形ABCD中∠B=90°,AB=9,BC=12,AD=8,CD=17.
已知,如图,四边形ABCD中∠B=90°,AB=9,BC=12,AD=8,CD=17.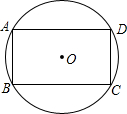 已知:如图,四边形ABCD内接于⊙O,且AB∥CD,AD∥BC,
已知:如图,四边形ABCD内接于⊙O,且AB∥CD,AD∥BC, 已知,如图,四边形ABCD是正方形,E、F分别是AB和AD延长线上的点,且BE=DF
已知,如图,四边形ABCD是正方形,E、F分别是AB和AD延长线上的点,且BE=DF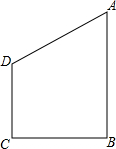 已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少?
已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少? 已知:如图,四边形ABCD及一点P.
已知:如图,四边形ABCD及一点P.