题目内容
(2012•眉山)如图,在与河对岸平行的南岸边有A、B、D三点,A、B、D三点在同一直线上,在A点处测得河对岸C点在北偏东60°方向;从A点沿河边前进200米到达B点,这时测得C点在北偏东30°方向,求河宽CD.
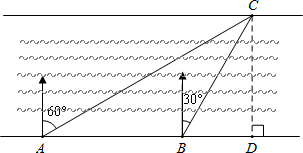

分析:首先由题意可得:∠CAB=90°-60°=30°,∠CBD=90°-30°=60°,AB=200米,CD⊥AB,则可证得△ABC是等腰三角形,即BC=AB,然后在Rt△CBD中,由CD=BC•sin60°,即可求得答案.
解答:解:根据题意得:∠CAB=90°-60°=30°,∠CBD=90°-30°=60°,AB=200米,CD⊥AB,
则∠ACB=∠CBD-∠CAB=60°-30°=30°,
则BC=AB=200米,
在Rt△CBD中,CD=BC•sin60°=200×
=100
(米).
答:河宽CD为100
米.
则∠ACB=∠CBD-∠CAB=60°-30°=30°,
则BC=AB=200米,
在Rt△CBD中,CD=BC•sin60°=200×
| ||
| 2 |
| 3 |
答:河宽CD为100
| 3 |
点评:此题考查了方向角问题.此题难度适中,注意能借助于解直角三角形的知识求解是解此题的关键,注意数形结合思想的应用.

练习册系列答案
相关题目
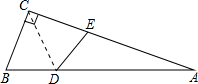 (2012•眉山)如图,在△ABC中,∠ACB=90°,∠A=20°,若将△ABC沿CD折叠,使B点落在AC边上的E处,则∠ADE的度数是( )
(2012•眉山)如图,在△ABC中,∠ACB=90°,∠A=20°,若将△ABC沿CD折叠,使B点落在AC边上的E处,则∠ADE的度数是( )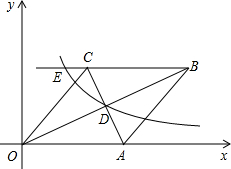 (2012•眉山)已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线
(2012•眉山)已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线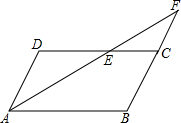 (2012•眉山)如图,平行四边形ABCD中,AB=5,AD=3,AE平分∠DAB交BC的延长线于F点,则CF=
(2012•眉山)如图,平行四边形ABCD中,AB=5,AD=3,AE平分∠DAB交BC的延长线于F点,则CF=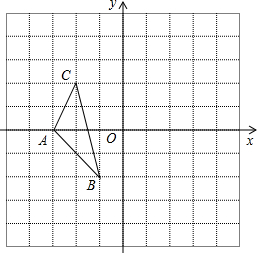 (2012•眉山)如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标分别为A(-3,0),B(-1,-2),C(-2,2).
(2012•眉山)如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标分别为A(-3,0),B(-1,-2),C(-2,2).