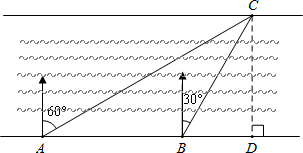
题目内容
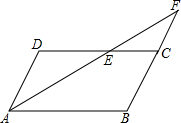（2012•眉山）如图，平行四边形ABCD中，AB=5，AD=3，AE平分∠DAB交BC的延长线于F点，则CF=2
2
．分析：根据角平分线的定义可得∠1=∠2，再根据两直线平行，内错角相等可得∠2=∠3，∠1=∠F，然后求出∠1=∠3，∠4=∠F，再根据等角对等边的性质可得AD=DE，CE=CF，根据平行四边形对边相等代入数据计算即可得解．
解答：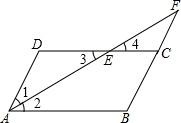
解：如图，∵AE平分∠DAB，
∴∠1=∠2，
平行四边形ABCD中，AB∥CD，AD∥BC，
∴∠2=∠3，∠1=∠F，
又∵∠3=∠4（对顶角相等），
∴∠1=∠3，∠4=∠F，
∴AD=DE，CE=CF，
∵AB=5，AD=3，
∴CE=DC-DE=AB-AD=5-3=2，
∴CF=2．
故答案为：2．
解：如图，∵AE平分∠DAB，∴∠1=∠2，
平行四边形ABCD中，AB∥CD，AD∥BC，
∴∠2=∠3，∠1=∠F，
又∵∠3=∠4（对顶角相等），
∴∠1=∠3，∠4=∠F，
∴AD=DE，CE=CF，
∵AB=5，AD=3，
∴CE=DC-DE=AB-AD=5-3=2，
∴CF=2．
故答案为：2．
点评：本题考查了平行四边形对边相等，对边平行的性质，角平分线的定义，平行线的性质，比较简单，熟记性质是解题的关键．
练习册系列答案
相关题目
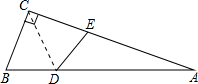（2012•眉山）如图，在△ABC中，∠ACB=90°，∠A=20°，若将△ABC沿CD折叠，使B点落在AC边上的E处，则∠ADE的度数是（ ）
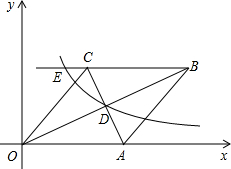（2012•眉山）已知：如图，在直角坐标系中，有菱形OABC，A点的坐标为（10，0），对角线OB、AC相交于D点，双曲线
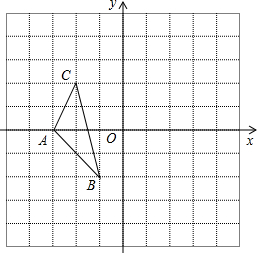（2012•眉山）如图，图中的小方格都是边长为1的正方形，△ABC的顶点坐标分别为A（-3，0），B（-1，-2），C（-2，2）．