题目内容
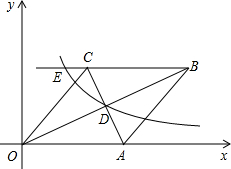 (2012•眉山)已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=
(2012•眉山)已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=| k |
| x |
①双曲线的解析式为y=
| 20 |
| x |
②E点的坐标是(4,8);
③sin∠COA=
| 4 |
| 5 |
④AC+OB=12
| 5 |
分析:过点C作CF⊥x轴于点F,由OB•AC=160可求出菱形的面积,由A点的坐标为(10,0)可求出CF的长,由勾股定理可求出OF的长,故可得出C点坐标,对角线OB、AC相交于D点可求出D点坐标,用待定系数法可求出双曲线y=
(x>0)的解析式,由反比例函数的解析式与直线BC的解析式联立即可求出E点坐标;由sin∠COA=
可求出∠COA的正弦值;根据A、C两点的坐标可求出AC的长,由OB•AC=160即可求出OB的长.
| k |
| x |
| CF |
| OC |
解答: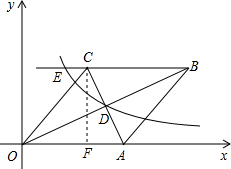 解:过点C作CF⊥x轴于点F,
解:过点C作CF⊥x轴于点F,
∵OB•AC=160,A点的坐标为(10,0),
∴OA•CF=
OB•AC=
×160=80,菱形OABC的边长为10,
∴CF=
=
=8,
在Rt△OCF中,
∵OC=10,CF=8,
∴OF=
=
=6,
∴C(6,8),
∵点D时线段AC的中点,
∴D点坐标为(
,
),即(8,4),
∵双曲线y=
(x>0)经过D点,
∴4=
,即k=32,
∴双曲线的解析式为:y=
(x>0),故①错误;
∵CF=8,
∴直线CB的解析式为y=8,
∴
,解得
,
∴E点坐标为(4,8),故②正确;
∵CF=8,OC=10,
∴sin∠COA=
=
=
,故③正确;
∵A(10,0),C(6,8),
∴AC=
=4
,
∵OB•AC=160,
∴OB=
=
=8
,
∴AC+OB=4
+8
=12
,故④正确.
故选C.
 解:过点C作CF⊥x轴于点F,
解:过点C作CF⊥x轴于点F,∵OB•AC=160,A点的坐标为(10,0),
∴OA•CF=
| 1 |
| 2 |
| 1 |
| 2 |
∴CF=
| 80 |
| OA |
| 80 |
| 10 |
在Rt△OCF中,
∵OC=10,CF=8,
∴OF=
| OC2-CF2 |
| 102-82 |
∴C(6,8),
∵点D时线段AC的中点,
∴D点坐标为(
| 10+6 |
| 2 |
| 8 |
| 2 |
∵双曲线y=
| k |
| x |
∴4=
| k |
| 8 |
∴双曲线的解析式为:y=
| 32 |
| x |
∵CF=8,
∴直线CB的解析式为y=8,
∴
|
|
∴E点坐标为(4,8),故②正确;
∵CF=8,OC=10,
∴sin∠COA=
| CF |
| OC |
| 8 |
| 10 |
| 4 |
| 5 |
∵A(10,0),C(6,8),
∴AC=
| (10-6)2+(0-8)2 |
| 5 |
∵OB•AC=160,
∴OB=
| 160 |
| AC |
| 160 | ||
4
|
| 5 |
∴AC+OB=4
| 5 |
| 5 |
| 5 |
故选C.
点评:本题考查的是反比例函数综合题,涉及到菱形的性质及反比例函数的性质、锐角三角函数的定义等相关知识,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
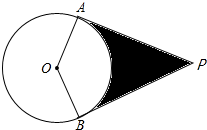 (2012•眉山)已知:PA、PB与⊙O相切于A点、B点,OA=1,PA=
(2012•眉山)已知:PA、PB与⊙O相切于A点、B点,OA=1,PA= (2012•眉山)已知:如图,四边形ABCD是正方形,BD是对角线,BE平分∠DBC交DC于E点,交DF于M,F是BC延长线上一点,且CE=CF.
(2012•眉山)已知:如图,四边形ABCD是正方形,BD是对角线,BE平分∠DBC交DC于E点,交DF于M,F是BC延长线上一点,且CE=CF.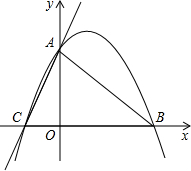 (2012•眉山)已知:如图,直线y=3x+3与x轴交于C点,与y轴交于A点,B点在x轴上,△OAB是等腰直角三角形.
(2012•眉山)已知:如图,直线y=3x+3与x轴交于C点,与y轴交于A点,B点在x轴上,△OAB是等腰直角三角形.