Question

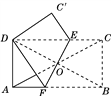
【题目】如图，在矩形纸片ABCD中，AC，BD相交于点O，AD∶AB＝1∶2，AC＝，将纸片折叠使点B与点D重合，求折叠后纸片重合部分的面积．

(

Answer 1

【答案】折叠后纸片重合部分的面积为.

【解析】试题分析：设AD＝x，则AB＝2x，根据勾股定理求得x的值，根据已知条件证明△ODE≌△OBF，根据全等三角形的性质可得DE＝BF，由折叠可知BF＝DF，设DE＝DF＝BF＝y，则AF＝2－y，在Rt△ADF中，由勾股定理列出方程求得y的值，即可求得折叠后纸片重合部分的面积．

试题解析：

设AD＝x，则AB＝2x.在矩形ABCD中，AB＝CD.

在Rt△ADC中，AC＝，AD2＋CD2＝AC2，

∴x2＋(2x)2＝()2.

解得x＝1(负根舍去)，即AD＝1，AB＝2.

在矩形ABCD中，OD＝OB，ED∥BF，

∴∠ODE＝∠OBF，∠OED＝∠OFB，

∴△ODE≌△OBF(AAS)，∴DE＝BF.

由折叠，得BF＝DF，∴DE＝DF＝BF.

设DE＝DF＝BF＝y，则AF＝2－y.

在Rt△ADF中，由勾股定理，得12＋(2－y)2＝y2.

解得y＝，即DE＝BF＝.

故S△DEF＝DE·AD＝××1＝.

∴折叠后纸片重合部分的面积为.