题目内容
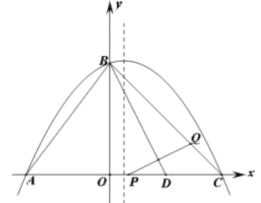
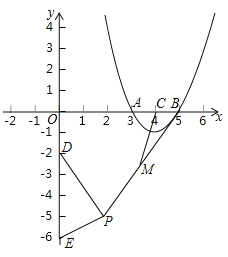
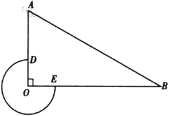
【题目】已知:如图一次函数y=![]() x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=
x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=![]() x2+bx+c的图象与一次函数y=
x2+bx+c的图象与一次函数y=![]() x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)
x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)
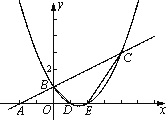
(1)求二次函数的解析式;
(2)求四边形BDEC的面积S;
(3)在x轴上是否存在点P,使得△PBC是以P为直角顶点的直角三角形?若存在,求出所有的点P,若不存在,请说明理由.
【答案】(1)y=![]() x2-
x2-![]() x+1
x+1
(2)![]()
(3)P的坐标为(1,0)或(3,0)
【解析】
解:(1)将B(0,1),D(1,0)的坐标代入y=![]() x2+bx+c得
x2+bx+c得
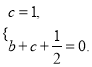
得解析式y=![]() x2-
x2-![]() x+1
x+1
(2)设C(x0,y0),则有
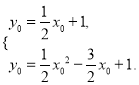
解得![]()
∴C(4,3).
由图可知:S=S△ACE-S△ABD.
又由对称轴为x=![]() 可知E(2,0).
可知E(2,0).
∴S=![]() AE·y0-
AE·y0-![]() AD×OB=
AD×OB=![]() ×4×3-
×4×3-![]() ×3×1=
×3×1=![]()
(3)设符合条件的点P存在,令P(a,0):
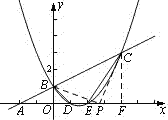
当P为直角顶点时,如图:过C作CF⊥x轴于F.
∵Rt△BOP∽Rt△PFC,
∴![]() .即
.即![]() .
.
整理得a2-4a+3=0.解得a=1或a=3
∴所求的点P的坐标为(1,0)或(3,0)
综上所述:满足条件的点P共有二个

【题目】“停课不停学,学习不延期”,某市通过教育资源公共服务平台和有线电视为全市中小学开设在线“空中课堂”,为了解学生每天的学习时间情况,在全市随机抽取了部分初中学生进行问卷调查,现将调查结果绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题:
组别 | 学习时间x(h) | 人数(人) |
A | 2.5<x≤3 | 40 |
B | 3<x≤3.5 | 170 |
C | 3.5<x≤4 | 350 |
D | 4<x≤4.5 | |
E | 4.5<x≤5 | 90 |
F | 5小时以上 | 50 |
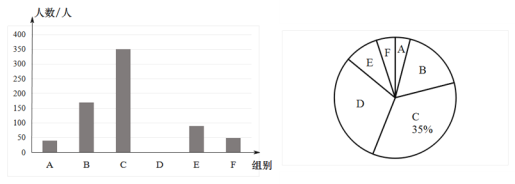
(1)这次参与问卷调查的初中学生有 人,中位数落在 组.
(2)补全条形统计图.
(3)若此市有初中学生2.8万人,求每天参与“空中课堂”学习时间3.5到4.5小时(不包括3.5小时)的初中学生有多少人?