题目内容
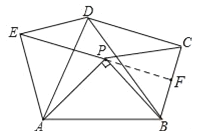
【题目】如图，△APB中，AB=2，∠APB=90°，在AB的同侧作正△ABD、正△APE和正△BPC，则四边形PCDE面积的最大值是 ．
【答案】1．
【解析】
试题分析：延长EP交BC于点F，∵∠APB=90°，∠AOE=∠BPC=60°，∴∠EPC=150°，∴∠CPF=180°﹣150°=30°，∴PF平分∠BPC，又∵PB=PC，∴PF⊥BC，设Rt△ABP中，AP=a，BP=b，则
CF=
CP=b，
，∵△APE和△ABD都是等边三角形，∴AE=AP，AD=AB，∠EAP=∠DAB=60°，∴∠EAD=∠PAB，∴△EAD≌△PAB（SAS），∴ED=PB=CP，同理可得：△APB≌△DCB（SAS），∴EP=AP=CP，∴四边形CDEP是平行四边形，∴四边形CDEP的面积=EP×CF=a×b=ab，又∵
≥0，∴2ab≤，∴ab≤1，即四边形PCDE面积的最大值为1．故答案为：1．
练习册系列答案
相关题目
