题目内容
今有一副三角板如图,中间各有一个直径为2cm的圆洞,现用三角板a的30°角那一头插入三角板b的圆洞中,则三角板a通过三角板b的圆洞那一部分的最大面积为( )cm2(不计三角板厚度)

A.2+
| B.2
| C.4 | D.4+
|

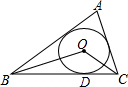
如图,
OA=OB=1,∠C=30°,OA⊥AC,OB⊥BC.
过A作AD⊥BC于D,作OF⊥AD于F,延长BO交CA于E.
则∠1=∠2=30°,所以OF=
,AF=
;
∴AD=1+
,则CD=
AD=
+
,CB=2+
.
在直角△OAE中,AE=
,OE=
,BE=1+
.
∴S△CBE=
×(2+
)(1+
)=2+
,
S△OAE=
×1×
=
,
所以四边形OACB的面积=2+
-
=2+
.
故选A.
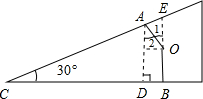
OA=OB=1,∠C=30°,OA⊥AC,OB⊥BC.
过A作AD⊥BC于D,作OF⊥AD于F,延长BO交CA于E.
则∠1=∠2=30°,所以OF=
| 1 |
| 2 |
| ||
| 2 |
∴AD=1+
| ||
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
在直角△OAE中,AE=
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
∴S△CBE=
| 1 |
| 2 |
| 3 |
2
| ||
| 3 |
7
| ||
| 6 |
S△OAE=
| 1 |
| 2 |
| ||
| 3 |
| ||
| 6 |
所以四边形OACB的面积=2+
7
| ||
| 6 |
| ||
| 6 |
| 3 |
故选A.


练习册系列答案
相关题目