Question

如图，已知△ABC的三个顶点坐标分别为A(－4，0)、B(1，0)、C(－2，6)．
(1)求经过A、B、C三点的抛物线解析式；
(2)设直线BC交y轴于点E，连接AE，求证：AE=CE;[来源:Z&xx&k.Com]
(3)设抛物线与y轴交于点D，连接AD交BC于点F，试问以A、B、F，为顶点的三角形与△ABC相似吗？
请说明理由．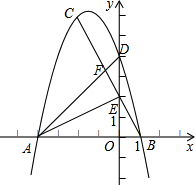

Answer 1

解：（1）∵抛物线经过A(－4，0)、B(1，0)，∴设函数解析式为：y=a（x＋4）（x－1）。
又∵由抛物线经过C（－2，6），∴6=a（－2＋4）（－2－1），解得： a=－1。
∴经过A、B、C三点的抛物线解析式为：y=－（x＋4）（x－1），即y=－x²－3x＋4。
（2）证明：设直线BC的函数解析式为y=kx+b，
由题意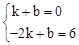得： ，解得：。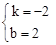
∴直线BC的解析式为y=－2x+2．
∴点E的坐标为（0，2）。
∴。
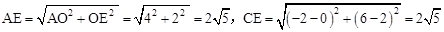∴AE=CE。
（3）相似。理由如下：
设直线AD的解析式为y=k₁x+b₁，则 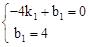，解得：。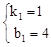
∴直线AD的解析式为y=x+4。
联立直线AD与直线BC的函数解析式可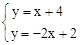得：，解得：。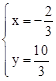
∴点F的坐标为（ ）。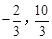
则。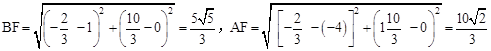
又∵AB=5，，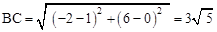
∴。∴。
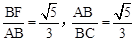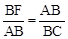又∵∠ABF=∠CBA，∴△ABF∽△CBA。
∴以A、B、F为顶点的三角形与△ABC相似。

解析