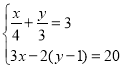题目内容
【题目】如图,四边形AOBC是正方形,OA=4,动点P从点O出发,沿折线OACB方向以1个单位/秒的速度匀速运动,另一个点Q从O出发,沿折线OBCA方向以2个单位/秒的速度匀速运动,运动时间为t秒,当它们相遇时停止运动,当以A、P、B、Q四点为顶点的四边形为平行四边形时,t的值为______.

【答案】![]()
【解析】
根据正方形的性质求出正方形的边长,再根据以A,P,B,Q四点为顶点的四边形是平行四边形可知,只有点P在OA上,点Q在BC上时符合,根据平行四边形的对边相等,分别表示出AP与BQ的长度,然后求解即可.
∵四边形AOBC是正方形,∴AO=AC,在RT△AOC中,OC=![]() ,
,
∴点C的坐标是(4![]() ,0),
,0),
∵P和Q运动到相遇时停止,且Q的运动速度比P快,正方形的边长是4,
∴只有点P在OA上,点Q在BC上时符合题意,如图所示,
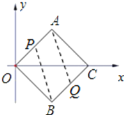
此时,AP=4-t,BQ=2t-4,
∵四边形APBQ是平行四边形,
∴AP=BQ,
∴4-t=2t-4,
解得t=![]() .
.
故答案为:![]() 秒.
秒.

练习册系列答案
相关题目