题目内容
如图,已知双曲线![]() 与直线y=
与直线y=![]() 交于A,B两点,点A在第一象限.试解答下列问题:
交于A,B两点,点A在第一象限.试解答下列问题:
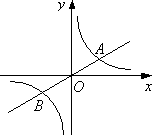
(1)若点A的坐标为(4,2),则点B的坐标为________;若点A的横坐标为m,则点B的坐标可表示为________;
(2)如图,过原点O作另一条直线l,交双曲线![]() 于P,Q两点,点P在第一象限.
于P,Q两点,点P在第一象限.
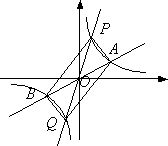
说明四边形APBQ一定是平行四边形;
设点A,P的横坐标分别为m,n,四边形APBQ可能是矩形吗?
可能是正方形吗?若可能,直接写出m,n应满足的条件;若不可能,请说明理由.
答案:
解析:
解析:
|
解:(1)(-4,-2)……(2分) (-m,-k'm)或(-m, (2)①由勾股定理OA= OB= ∴OA=OB 同理可得OP=OQ, 所以四边形APBQ一定是平行四边形.……(2分) ②四边形APBQ可能是矩形……(1分) m,n应满足的条件是mn=k……(1分) 四边形APBQ不可能是正方形……(1分) 理由:点A,P不可能达到坐标轴,即∠POA≠900.……(1分) |

练习册系列答案
相关题目
 如图,在平面直角坐标系中,直
如图,在平面直角坐标系中,直 探索函数
探索函数 如图,在平面直角坐标系中,直
如图,在平面直角坐标系中,直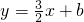 与双曲线
与双曲线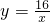 相交于第一象限内的点A,AB、AC分别垂直于x轴、y轴,垂足分别为B、C,已知四边形ABCD是正方形,求直线所对应的一次函数的解析式以及它与x轴的交点E的坐标.
相交于第一象限内的点A,AB、AC分别垂直于x轴、y轴,垂足分别为B、C,已知四边形ABCD是正方形,求直线所对应的一次函数的解析式以及它与x轴的交点E的坐标.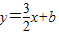 与双曲线
与双曲线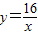 相交于第一象限内的点A,AB、AC分别垂直于x轴、y轴,垂足分别为B、C,已知四边形ABCD是正方形,求直线所对应的一次函数的解析式以及它与x轴的交点E的坐标.
相交于第一象限内的点A,AB、AC分别垂直于x轴、y轴,垂足分别为B、C,已知四边形ABCD是正方形,求直线所对应的一次函数的解析式以及它与x轴的交点E的坐标.