题目内容
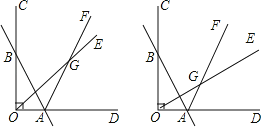
【题目】已知如图,∠COD=90°,直线AB与OC交于点B,与OD交于点A,射线OE和射线AF交于点G.
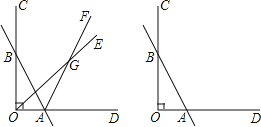
(1)若OE平分∠BOA,AF平分∠BAD,∠OBA=30°,则∠OGA=
(2)若∠GOA=![]() ∠BOA,∠GAD=
∠BOA,∠GAD=![]() ∠BAD,∠OBA=30°,则∠OGA=
∠BAD,∠OBA=30°,则∠OGA=
(3)将(2)中“∠OBA=30°”改为“∠OBA=α”,其余条件不变,则∠OGA= (用含α的代数式表示)
(4)若OE将∠BOA分成1:2两部分,AF平分∠BAD,∠ABO=α(30°<α<90°),求∠OGA的度数(用含α的代数式表示)
【答案】(1)15°;(2)10°;(3)![]() ;(4)
;(4)![]() α+15°或
α+15°或![]() α﹣15°;
α﹣15°;
【解析】
试题分析:(1)由于∠BAD=∠ABO+∠BOA=α+90°,由AF平分∠BAD得到∠FAD=![]() ∠BAD,而∠FAD=∠EOD+∠OGA,2×45°+2∠OGA=α+90°,则∠OGA=
∠BAD,而∠FAD=∠EOD+∠OGA,2×45°+2∠OGA=α+90°,则∠OGA=![]() α,然后把α=30°代入计算即可;
α,然后把α=30°代入计算即可;
(2)由于∠GOA=![]() ∠BOA=30°,∠GAD=
∠BOA=30°,∠GAD=![]() ∠BAD,∠OBA=α,根据∠FAD=∠EOD+∠OGA得到3×30°+3∠OGA=α+90°,则∠OGA=
∠BAD,∠OBA=α,根据∠FAD=∠EOD+∠OGA得到3×30°+3∠OGA=α+90°,则∠OGA=![]() α,然后把α=30°代入计算;
α,然后把α=30°代入计算;
(3)由(2)得到∠OGA=![]() α;
α;
(4)讨论:当∠EOD:∠COE=1:2时,利用∠BAD=∠ABO+∠BOA=α+90°,∠FAD=∠EOD+∠OGA得到2×30°+2∠OGA=α+90°,则∠OGA=![]() α+15°;
α+15°;
当∠EOD:∠COE=2:1时,则∠EOD=60°,同理得∠OGA=![]() α﹣15°.
α﹣15°.
解:(1)15°;
(2)10°;
(3)![]() ;
;
(4)当∠EOD:∠COE=1:2时,
则∠EOD=30°,
∵∠BAD=∠ABO+∠BOA=α+90°,
而AF平分∠BAD,
∴∠FAD=![]() ∠BAD,
∠BAD,
∵∠FAD=∠EOD+∠OGA,
∴2×30°+2∠OGA=α+90°,
∴∠OGA=![]() α+15°;
α+15°;
当∠EOD:∠COE=2:1时,则∠EOD=60°,
同理得到∠OGA=![]() α﹣15°,
α﹣15°,
即∠OGA的度数为![]() α+15°或
α+15°或![]() α﹣15°.
α﹣15°.
故答案为15°,10°,![]() α.
α.

 阅读快车系列答案
阅读快车系列答案