题目内容
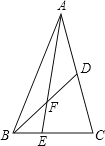
【题目】如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=12,则S△ADF﹣S△BEF= .
【答案】2;
【解析】
试题分析:S△ADF﹣S△BEF=S△ABD﹣S△ABE,所以求出三角形ABD的面积和三角形ABE的面积即可,因为EC=2BE,点D是AC的中点,且S△ABC=12,就可以求出三角形ABD的面积和三角形ABE的面积.
解:∵点D是AC的中点,
∴AD=![]() AC,
AC,
∵S△ABC=12,
∴S△ABD=![]() S△ABC=
S△ABC=![]() ×12=6.
×12=6.
∵EC=2BE,S△ABC=12,
∴S△ABE=![]() S△ABC=
S△ABC=![]() ×12=4,
×12=4,
∵S△ABD﹣S△ABE=(S△ADF+S△ABF)﹣(S△ABF+S△BEF)=S△ADF﹣S△BEF,
即S△ADF﹣S△BEF=S△ABD﹣S△ABE=6﹣4=2.
故答案为:2.

练习册系列答案
相关题目
【题目】小洪根据演讲比赛中九位评委所给的分数制作了如下表格:
平均数 | 中位数 | 众数 | 方差 |
8.5 | 8.3 | 8.1 | 0.15 |
如果去掉一个最高分和一个最低分,那么表格中数据一定不发生变化的是( ).
A.平均数 B.中位数 C.众数 D.方差