��Ŀ����
����Ŀ����֪����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��![]() ��x�ᡢy��Ľ���ֱ�ΪA��B������OBA���ۣ�ʹ��O�Ķ�Ӧ��H����ֱ��AB�ϣ��ۺ۽�x���ڵ�C��
��x�ᡢy��Ľ���ֱ�ΪA��B������OBA���ۣ�ʹ��O�Ķ�Ӧ��H����ֱ��AB�ϣ��ۺ۽�x���ڵ�C��
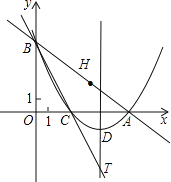
��1��ֱ��д����C�����꣬�����A��B��C����������ߵĽ���ʽ��
��2���������ߵĶ���ΪD����ֱ��BC���Ƿ���ڵ�P��ʹ���ı���ODAPΪƽ���ı��Σ������ڣ������P�����ꣻ�������ڣ�˵�����ɣ�
��3���������ߵĶԳ�����ֱ��BC�Ľ���ΪT��QΪ�߶�BT��һ�㣬ֱ��д��|QA��QO|��ȡֵ��Χ��
���𰸡���1����C������Ϊ��3��0����![]() ����2��ֱ��BC�ϲ����ڷ��������ĵ�P�����ɼ�������3��0��|QA��QO|��4��
����2��ֱ��BC�ϲ����ڷ��������ĵ�P�����ɼ�������3��0��|QA��QO|��4��
��������
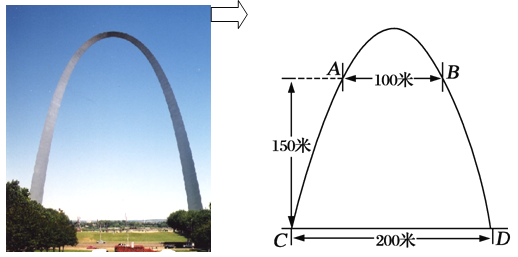
�����������1������ֱ��![]() �ֱ������A��B��������Ȼ�����ù��ɶ��������������ε���������߶�OC�ij����ɵõ���C�����꣬Ȼ�����ô���ϵ��������������ߵĽ���ʽ����2������ƽ���ı��ε�����������������ĵ�P�����꣬Ȼ�����ֱ��BC�Ľ���ʽΪy=��2x+6���鼴�ɣ���3����QA=QOʱ��|QA��QO|��ֵ��С=0����Q��AH���ӳ�����ֱ��BC����ʱ����ʱ|QA��QO|���=4.
�ֱ������A��B��������Ȼ�����ù��ɶ��������������ε���������߶�OC�ij����ɵõ���C�����꣬Ȼ�����ô���ϵ��������������ߵĽ���ʽ����2������ƽ���ı��ε�����������������ĵ�P�����꣬Ȼ�����ֱ��BC�Ľ���ʽΪy=��2x+6���鼴�ɣ���3����QA=QOʱ��|QA��QO|��ֵ��С=0����Q��AH���ӳ�����ֱ��BC����ʱ����ʱ|QA��QO|���=4.
�����������1����C��������3��0����
�ߵ�A��B������ֱ�ΪA��8��0����B��0��6����
������A��B��C����������ߵĽ���ʽΪy=a��x��3����x��8����
��x=0��y=6���������ߵĽ���ʽ����![]() ��
��
���A��B��C����������ߵĽ���ʽΪ![]() ��
��
��2���ɵ������ߵĶԳ���Ϊֱ��![]() ������D������Ϊ
������D������Ϊ![]() ��
��
�������ߵĶԳ�����x��Ľ���ΪG��
ֱ��BC�Ľ���ʽΪy=��2x+6.
�ⷨһ��
��ͼ��ȡOA���е�E��
����D���ڵ�E�ĶԳƵ�P����PN��x���ڵ�N��
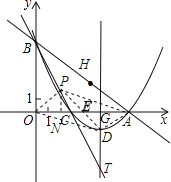
���PEN=��DEG����PNE=��DGE��PE=DE��
�ɵá�PEN�ա�DEG��
��![]() ���ɵ�E�������Ϊ��4��0����
���ɵ�E�������Ϊ��4��0����
NE=EG=![]() ��ON=OE��NE=
��ON=OE��NE=![]() ��NP=DG=
��NP=DG=![]() ��
��
���P������Ϊ![]() ��
��
��x=![]() ʱ��
ʱ��![]() �� ���P����ֱ��BC�ϣ�
�� ���P����ֱ��BC�ϣ�
��ֱ��BC�ϲ����ڷ��������ĵ�P��
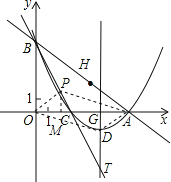
�ⷨ������ͼ����OP��AD��ֱ��BC�ڵ�P��
����AP����PM��x���ڵ�M��
��OP��AD��
���POM=��GAD��tan��POM=tan��GAD����![]() ��
��
�� �� ���
�� ���![]() �� ������
�� ������![]() ��ԭ���̵Ľ⣮
��ԭ���̵Ľ⣮
��ʱ��P������Ϊ![]() ��
��
����ʱ![]() ��OM��GA��
��OM��GA��
��![]() ��
��
��OP��AD�����ı��εĶԱ�OP��ADƽ�е�����ȣ�
��ֱ��BC�ϲ����ڷ��������ĵ�P��
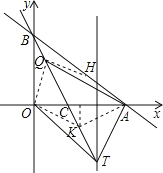
��3��|QA��QO|��ȡֵ��Χ��![]() ��
��
��Q��OA�Ĵ�ֱƽ��������ֱ��BC�Ľ���ʱ�������K������
��ʱOK=AK����|QA��QO|=0��
��Q��AH���ӳ�����ֱ��BC����ʱ����ʱ|QA��QO|���
ֱ��AH�Ľ���ʽΪ��y=��![]() x+6��ֱ��BC�Ľ���ʽΪ��y=��2x+6��
x+6��ֱ��BC�Ľ���ʽΪ��y=��2x+6��
�����ɵã�����Ϊ��0��6������OQ=6��AQ=10����|QA��QO|=4��
��|QA��QO|��ȡֵ��Χ�ǣ�0��|QA��QO|��4��