题目内容
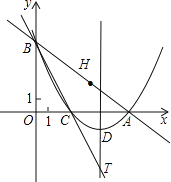
【题目】如图,已知抛物线y=![]() 与x轴交于A、B两点.
与x轴交于A、B两点.
(1)点A的坐标是 ,点B的坐标是 ,抛物线的对称轴是直线 ;
(2)将抛物线向上平移m个单位,与x轴交于C、D两点(点C 在点D的左边).若CD:AB=3:4,求m的值;
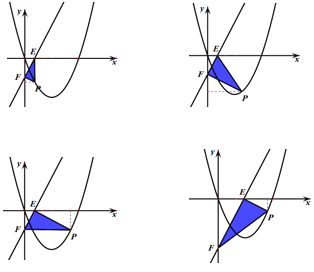
(3)点P是(2)中平移后的抛物线上y轴右侧部分的点,直线y=2x+b(b![]() 0)与 x、y轴分别交于点E、F.若以EF为直角边的三角形PEF与△OEF相似,直接写出点P的坐标.
0)与 x、y轴分别交于点E、F.若以EF为直角边的三角形PEF与△OEF相似,直接写出点P的坐标.
【答案】(1)、A(-![]() ,0), B(
,0), B(![]() ,0) x=
,0) x=![]() ;(2)、m=
;(2)、m=![]() ;(3)、(
;(3)、(![]() ,
,![]() )、(
)、(![]() ,
,![]() )、(2,-2)、(
)、(2,-2)、(![]() ,
,![]() )
)
【解析】
试题分析:(1)、根据二次函数的性质求出与x轴的交点以及对称轴;(2)、根据题意得出AB=4,从而得出CD的长度,然后计算出点C和D的坐标,从而得出m的值;(3)、根据题意画出图形,得出答案.
试题解析:(1)、A(-![]() ,0), B(
,0), B(![]() ,0) x=
,0) x=![]()
(2)、由(1)知,AB=4 ∵CD:AB=3:4 ∴CD=3 ∵y=![]() 向上平移m个单位
向上平移m个单位
∴C (0,0), D(3,0) ∴y=![]() -3x ∴m=
-3x ∴m=![]() .
.
(3)、(![]() ,
,![]() )、(
)、(![]() ,
,![]() )、(2,-2)、(
)、(2,-2)、(![]() ,
,![]() )
)

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目