题目内容
【题目】如图，PA、PB分别切圆O于A、B两点，C为劣弧AB上一点，∠APB=40°，则∠ACB=（ ）．
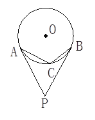
A.70°B.80°C.110°D.140°
【答案】C
【解析】
如图，连接AO，OB，PA、PB分别切圆O于A、B两点，可以知道∠PAO=∠PBO=90°，由此可以求出∠AOB的度数；设点E是优弧AB上一点，由圆周角定理知，∠E=70°，由圆内接四边形的对角互补即可求出∠ACB的度数．
如图，连接AO，OB，
∵PA、PB分别切圆O于A、B两点，
∴∠PAO=∠PBO=90°，
∴∠AOB=180°-∠APB=140°，
设点E是优弧AB上一点，
由圆周角定理知，∠E=70°，
由圆内接四边形的对角互补知，
∠ACB=180°-∠E=110°．
故选：C．
练习册系列答案
相关题目
【题目】甲、乙、丙三位运动员在相同条件下各射靶10次，每次射靶的成绩如下：
甲：9，10，8，5，7，8，10，8，8，7；
乙：5，7，8，7，8，9，7，9，10，10；
丙：7，6，8，5，4，7，6，3，9，5.
（1）根据以上数据完成下表：
平均数 | 中位数 | 方差 | |
甲 | 8 | 8 | |
乙 | 8 | 8 | 2.2 |
丙 | 6 | 3 |
（2）依据表中数据分析，哪位运动员的成绩最稳定，并简要说明理由；
（3）比赛时三人依次出场，顺序由抽签方式决定.求甲、乙相邻出场的概率.
