题目内容
【题目】下列数阵是由偶数排列而成的:
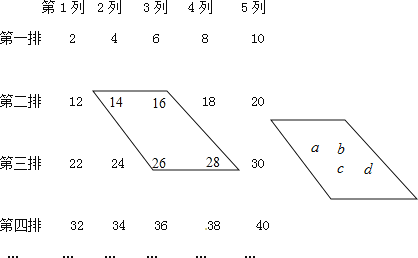
(1)在数阵中任意作一类似的框,如果这四个数的和为188,能否求出这四个数?如果能,求出这些数,如果不能,说明理由.如果和为288,能否求出这四个数?说明理由.
(2)有理数110在上面数阵中的第 排、第 列.
【答案】(1)四个数的和不能是288;(2)11,5.
【解析】
试题分析:(1)可利用图例,看出框内四个数字之间的关系,上下相差10,左右相差2,用含a的代数式分别表示b,c,d,根据这四个数的和为188列出方程,求解即可;
(2)观察数阵可以得到,整10的数都在第5列,第5列的第一排是10,第二排是20,…,依此求解即可.
解:(1)如果这四个数的和为188,能求出这四个数.理由如下:
∵a+b+c+d=188,
∴a+a+2+a+12+a+14=188,
∴a=40,
∴这四个数是:40,42,52,54;
如果和为288,不能求出这四个数.理由如下:
∵a+b+c+d=288,
∴a+a+2+a+12+a+14=288,
∴a=65,
∵65不是偶数,
∴四个数的和不能是288;
(2)∵整10的数都在第5列,第5列的第一排是10,第二排是20,…,
∴110在上面数阵中的第11排第5列.
故答案为:11,5.

练习册系列答案
相关题目