题目内容
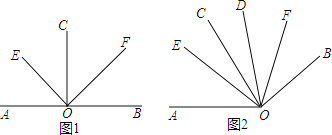
【题目】(1)如图1,若CO⊥AB,垂足为O,OE、OF分别平分∠AOC与∠BOC.求∠EOF的度数;
(2)如图2,若∠AOC=∠BOD=80°,OE、OF分别平分∠AOD与∠BOC.求∠EOF的度数;
(3)若∠AOC=∠BOD=α,将∠BOD绕点O旋转,使得射线OC与射线OD的夹角为β,OE、OF分别平分∠AOD与∠BOC.若α+β≤180°,α>β,则∠EOC= .(用含α与β的代数式表示)
【答案】(1)90°;(2)80°;(3)![]()
【解析】
试题分析:(1)根据垂直的定义得到∠AOC=∠BOC=90°,根据角平分线的定义即可得到结论;
(2)根据角平分线的定义得到∠EOD=![]() ∠AOD=
∠AOD=![]() ×(80+β)=40+
×(80+β)=40+![]() β,∠COF=
β,∠COF=![]() ∠BOC=
∠BOC=![]() ×(80+β)=40+
×(80+β)=40+![]() β,根据角的和差即可得到结论;
β,根据角的和差即可得到结论;
(3)如图2由已知条件得到∠AOD=α+β,根据角平分线的定义得到∠DOE=![]() (α+β),即可得到结论.
(α+β),即可得到结论.
解:(1)∵CO⊥AB,
∴∠AOC=∠BOC=90°,
∵OE平分∠AOC,
∴∠EOC=![]() ∠AOC=
∠AOC=![]() ×90°=45°,
×90°=45°,
∵OF平分∠BOC,
∴∠COF=![]() ∠BOC=
∠BOC=![]() ×90°=45°,
×90°=45°,
∠EOF=∠EOC+∠COF=45°+45°=90°;
(2)∵OE平分∠AOD,
∴∠EOD=![]() ∠AOD=
∠AOD=![]() ×(80+β)=40+
×(80+β)=40+![]() β,
β,
∵OF平分∠BOC,
∴∠COF=![]() ∠BOC=
∠BOC=![]() ×(80+β)=40+
×(80+β)=40+![]() β,
β,
∠COE=∠EOD﹣∠COD=40+![]() β﹣β=40﹣
β﹣β=40﹣![]() β;
β;
∠EOF=∠COE+∠COF=40﹣![]() β+40+
β+40+![]() β=80°;
β=80°;
(3)如图2,∵∠AOC=∠BOD=α,∠COD=β,
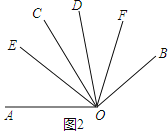
∴∠AOD=α+β,
∵OE平分∠AOD,
∴∠DOE=![]() (α+β),
(α+β),
∴∠COE=∠DOE﹣∠COD=![]() =
=![]() ,
,
如图3,∵∠AOC=∠BOD=α,∠COD=β,
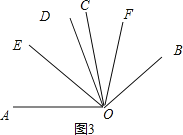
∴∠AOD=α+β,
∵OE平分∠AOD,
∴∠DOE=![]() (α﹣β),
(α﹣β),
∴∠COE=∠DOE+∠COD=![]() .
.
综上所述:![]() ,
,
故答案为:![]() .
.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案