Question

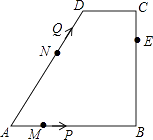
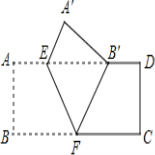
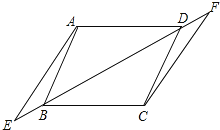
【题目】如图，已知点E、F在四边形ABCD的对角线BD所在的直线上，且BE=DF，AE∥CF，请再添加一个条件（不要在图中再增加其它线段和字母），能证明四边形ABCD是平行四边形，并证明你的想法.

你所添加的条件：____________________________________；

证明：

Answer 1

【答案】AE=CF

【解析】

试题要证四边形ABCD是平行四边形，只要得出一组对边（AB和CD）平行且相等即可，即只要添加一个条件使得△ABE≌△CDF，由已知可得两三角形全等的条件有∠E＝∠F，BE＝DF，故可添加AE＝CF（答案不唯一），利用SAS证明△ABE≌△CDF．

试题解析：答案不唯一，例如：添加AE＝CF．

证明如下：

∵AE∥CF，

∴∠E＝∠F，

又BE＝DF，AE＝CF，

∴△ABE≌△CDF（SAS），

∴AB＝CD，∠ABE＝∠CDF，

∴∠ABD＝∠CDB，

∴AB∥CD，

∴四边形ABCD是平行四边形．