题目内容
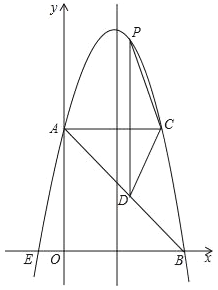
【题目】如图,在平面直角坐标系中,抛物线y=ax2+4x+c与y轴交于点A(0,5),与x轴交于点E,B,点B坐标为(5,0).
(1)求二次函数解析式及顶点坐标;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
【答案】(1)y=﹣x2+4x+5,顶点坐标为(2,9);(2)当P(![]() ,
, ![]() )时,S有最大值为
)时,S有最大值为![]() .
.
【解析】试题分析:(1)用待定系数法求抛物线解析式,并利用配方法求顶点坐标;
(2)先求出直线AB解析式,设出点P坐标(x,-x2+4x+5),建立函数关系式S四边形APCD=-2x2+10x,根据二次函数求出极值;可得P的坐标.
试题解析:(1)把点A(0,5),点B坐标为(5,0)代入抛物线y=ax2+4x+c中,
得: ![]() ,解得:
,解得: ![]() ,
,
∴抛物线的解析式为:y=-x2+4x+5=-(x-2)2+9,
∴顶点坐标为(2,9);
(2)设直线AB的解析式为:y=mx+n,
∵A(0,5),B(5,0),
∴![]() ,
,
解得: ![]() ,
,
∴直线AB的解析式为:y=-x+5,
设P(x,-x2+4x+5),则D(x,-x+5),
∴PD=(-x2+4x+5)-(-x+5)=-x2+5x,
∵点C在抛物线上,且纵坐标为5,
∴C(4,5),
∴AC=4,
∴S四边形APCD=![]() ACPD=
ACPD=![]() ×4(-x2+5x)=-2x2+10x=-2(x-
×4(-x2+5x)=-2x2+10x=-2(x-![]() )2+
)2+![]() ,
,
∵-2<0,
∴S有最大值,
∴当x=![]() 时,S有最大值为
时,S有最大值为![]() ,
,
此时P(![]() ,
, ![]() ).
).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目