题目内容
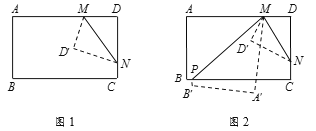
【题目】如图1,在矩形ABCD中,AB=6cm,BC=8cm,E、F分别是AB、BD的中点,连接EF,点P从点E出发,沿EF方向匀速运动,速度为1cm/s,同时,点Q从点D出发,沿DB方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s,解答下列问题:
(1)求证:△BEF∽△DCB;
(2)当点Q在线段DF上运动时,若△PQF的面积为0.6cm2,求t的值;
(3)当t为何值时,△PQF为等腰三角形?试说明理由.

【答案】(1)见解析;(2) t=![]() 或t=2秒;(3)见解析.
或t=2秒;(3)见解析.
【解析】分析:![]() 根据两组角对应相等的两个三角形相似即可证明.
根据两组角对应相等的两个三角形相似即可证明.
![]() 用
用![]() 表示出
表示出![]() ,列方程求解即可.
,列方程求解即可.
![]() 分4种情况进行讨论.
分4种情况进行讨论.
详解:(1)∵四边形ABCD是矩形,
∴![]() AD∥BC,
AD∥BC,![]()
在![]() 中,
中,![]()
∵![]() 别是
别是![]() 的中点,
的中点,
∴EF∥AD,![]()
∴![]() EF∥BC,
EF∥BC,
∴![]()
∴![]()
(2)如图1,过点Q作![]() 于
于![]() ,
,
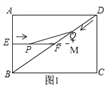
∴QM∥BE,
∴![]()
![]()
![]()
![]()
∴![]()
∴![]() (舍)或
(舍)或![]() 秒;
秒;
(3)当点Q在DF上时,如图2,![]()
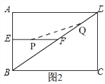
∴![]()
∴![]() .
.
当点Q在BF上时,![]() ,如图3,
,如图3,
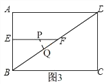
∴![]()
∴![]()
![]() 时,如图4,
时,如图4,
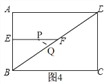
∴![]()
∴![]()
![]() 时,如图5,
时,如图5,
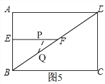
∴![]()
∴![]()
综上所述,t=1或3或![]() 或
或![]() 秒时,△PQF是等腰三角形.
秒时,△PQF是等腰三角形.

练习册系列答案
相关题目