题目内容
【题目】已知：如图，在ABCD中，DE平分∠ADB，交AB于E，BF平分∠CBD，交CD于F．
（1）求证：△ADE≌△CBF；
（2）当AD与BD满足什么关系时，四边形DEBF是矩形？请说明理由．
【答案】见解析
【解析】
（1）根据平行四边形的性质得出AD=BC，∠A=∠C，AD∥BC，进而得出∠ADE=∠CBF，利用全等三角形的判定证明即可；
（2）利用矩形的判定解答即可．
（1）∵ABCD，∴AD=BC，∠A=∠C，AD∥BC，∴∠ADB=∠CBD．
∵DE平分∠ADB，BF平分∠CBD，∴∠ADE=∠CBF=∠BDE=∠DBF．在△ADE与△CBF中，∵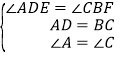
，∴△ADE≌△CBF（ASA）；
（2）当AD=BD时．理由如下：
∵DE平分∠ADB，∴DE⊥BE，∴∠DEB=90°．
∵△ADE≌△CBF，∴DE=BF．
∵∠EDB=∠DBF，∴DE∥BF，∴四边形DEBF是平行四边形．
∵∠DEB=90°，∴平行四边形DEBF是矩形．
练习册系列答案
相关题目
