题目内容
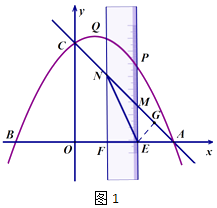
【题目】如图,已知抛物线 ![]() 与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,有一宽度为1的刻度尺沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q,交直线AC于点M和点N,交x轴于点E和点F.
与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,有一宽度为1的刻度尺沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q,交直线AC于点M和点N,交x轴于点E和点F.
(1)求点A、B、C的坐标;
(2)当点M和点N都在线段AC上时,连接EN,如果点E的坐标为(4,0),求sin∠ANE的值;
(3)在刻度尺平移过程中,当以点P、Q、N、M为顶点的四边形是平行四边形时,求点N的坐标.
【答案】
(1)
解:令y=0得: ![]() =0,解得x=5或x=﹣3.
=0,解得x=5或x=﹣3.
∵点A在点B的右侧,
∴点A、B的坐标分为(5,0)、(﹣3,0).
当x=0时,y=5,
∴点C的坐标为(0,5)
(2)
解:如图1,作EG⊥AC,垂足为点G.
∵点E的坐标为(4,0),
∴OE=4.
∵OA=OC=5,
∴AE=1,∠OAC=45°.
∴AF=FN=2,GE=AEsin45°= ![]()
在Rt△EFN中,依据勾股定理可知NE= ![]() =
= ![]() ,
,
∴sin∠ANE= ![]() =
= ![]() =
= ![]()
(3)
解:设直线AC的函数表达式为y=kx+b.
将点A和点C的坐标代入得: ![]() ,
,
解得k=﹣1,b=5.
∴直线AC的函数表达式为y=﹣x+5.
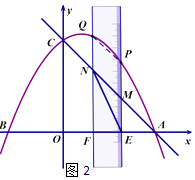
①当MN为边时,如图2所示:
设点Q(n, ![]() ),
),
则点P(n+1, ![]() ),点N(n,﹣n+5)M(n+1,﹣n+4).
),点N(n,﹣n+5)M(n+1,﹣n+4).
∵QN=PM
∴ ![]() ,解得n=2.
,解得n=2.
∴点N的坐标为(2,3).
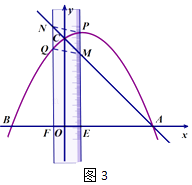
②当MN是平行四边形的对角线时,如图3所示:
设点F的坐标为(m,0),
则N(m,﹣m+5),M(m+1,﹣m+4),
Q(m, ![]() ),P(m+1,
),P(m+1, ![]() ).
).
∵QN=PM,
∴ ![]() ,解得m=2±
,解得m=2± ![]() .
.
∴点N的坐标为(2+ ![]() ,3﹣
,3﹣ ![]() )或(2﹣
)或(2﹣ ![]() ,3+
,3+ ![]() ).
).
综上所述,以点P、Q、N、M为顶点的四边形是平行四边形时,点N的坐标为(2,3)
或(2+ ![]() ,3﹣
,3﹣ ![]() )或(2﹣
)或(2﹣ ![]() ,3+
,3+ ![]() )
)
【解析】(1)利用坐标轴上点的坐标特征即可结论;(2)先确定出AF=FN=2,GE= ![]() ,再利用勾股定理求出NE=
,再利用勾股定理求出NE= ![]() ,即可得出结论;(3)先确定出直线AC的函数表达式为y=﹣x+5.再分MN为边和对角线两种情况,建立方程求解即可得出结论.
,即可得出结论;(3)先确定出直线AC的函数表达式为y=﹣x+5.再分MN为边和对角线两种情况,建立方程求解即可得出结论.
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案,需要熟知二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 阅读快车系列答案
阅读快车系列答案【题目】某旅行社拟在暑假期间面向学生推出“林州红旗渠一日游”活动,
收费标准如下:
人数m | 0<m≤100 | 100<m≤200 | m>200 |
收费标准(元/人) | 90 | 85 | 75 |
甲、乙两所学校计划组织本校学生自愿参加此项活动.已知甲校报名参加的学生人数多于100人,乙校报名参加的学生人数少于100人.经核算,若两校分别组团共需花费10 800元,若两校联合组团只需花赞18 000元.
(1)两所学校报名参加旅游的学生人数之和超过200人吗? 为什么?
(2)两所学校报名参加旅游的学生各有多少人?