题目内容
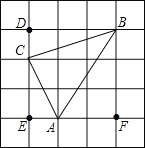
【题目】如图,方格中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求:
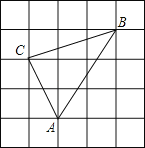
(1)△ABC的周长;
(2)请判断三角形ABC是否是直角三角形,并说明理由;
(3)△ABC的面积;
(4)点C到AB边的距离.
【答案】(1)![]() ;(2)△ABC不是直角三角形,理由见解析;(3)
;(2)△ABC不是直角三角形,理由见解析;(3)![]() ;(4)
;(4)![]()
【解析】
(1)根据勾股定理求出△ABC的三条边长,再将三条边长相加即可得出该三角形的周长;
(2)根据勾股定理的逆定理判定即可;
(3)利用图形知S△ABC=S正方形BDEF﹣S△BCD﹣S△ACE﹣S△ABF;
(4)设点C到AB的距离是h,则根据三角形的面积公式知![]() ABh=
ABh=![]() ,据此可以求得h的值.
,据此可以求得h的值.
(1)根据勾股定理知,BC=![]() =
=![]() ,AC=
,AC=![]() =
=![]() ,AB=
,AB=![]() =
=![]() ,
,
故△ABC的周长=AB+BC+AC=![]()
![]() ;
;
(2)△ABC不是直角三角形,理由如下:
由(1)可知,BC=![]() ,AC=
,AC=![]() ,AB=
,AB=![]() ,AC<BC<AB,
,AC<BC<AB,
∵![]() ,
,
∴△ABC不是直角三角形;
(3)如图,
S△ABC=S正方形BDEF﹣S△BCD﹣S△ACE﹣S△ABF
=3×3﹣![]() ×1×3﹣
×1×3﹣![]() ×1×2﹣
×1×2﹣![]() ×2×3
×2×3
=![]() ;
;
(3)设点C到AB的距离是h.
由(3)知,三角形ABC的面积是![]() ,则
,则![]() ABh=
ABh=![]() ,即
,即![]() ×
×![]() h=
h=![]() ,
,
解得,h=![]() ,即点C到AB的距离为
,即点C到AB的距离为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目