题目内容
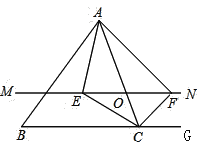
【题目】(1)如图 ,∠AOB=∠COD=90°
①∠AOD=30°求∠BOC
②若∠AOD=α求用α的代数式表示∠BOC.

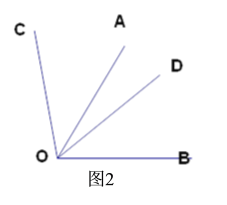
(2)如图2,若∠AOB=∠COD=60°,直接写出∠AOC与∠BOD的关系.
【答案】(1)①150°;②180°-α;(2)∠AOC=∠BOD.
【解析】
(1)①根据∠AOB=∠COD=90°,∠AOD=30°,∠AOC =∠COD-∠AOD=60°,进而求出∠BOC;
②根据∠AOB=∠COD=90°,∠AOD=α,∠AOC =∠COD-∠AOD=90°-α,进而求出∠BOC;;
(2)将∠AOB=∠COD=60°,写成∠AOD+∠BOD=∠AOD+∠AOC=60°,即可得出结论.
(1)①∵∠AOB=∠COD=90°,∠AOD=30°,
∴∠BOC=∠AOB+∠AOC
=∠AOB+(∠COD-∠AOD)
=90°+(90°-30°)
=150°;
②∵∠AOB=∠COD=90°,∠AOD=α,
∴∠BOC=∠AOB+∠AOC
=∠AOB+(∠COD-∠AOD)
=90°+(90°-α)
=180°-α;
(2)∠AOC=∠BOC,理由是:
∵∠AOB=∠COD=60°,
∴∠AOD+∠BOD=∠AOD+∠AOC,
∴∠AOC=∠BOD.

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目