Question

【题目】探究题：

(1)三条直线相交，最少有 个交点；最多有 个交点，画出图形，并数出图形中的对顶角和邻补角的对数；

(2)四条直线相交，最少有 个交点；最多有 个交点，画出图形，并数出图形中的对顶角和邻补角的对数；

(3)依次类推，n条直线相交，最少有 个交点；最多有 个交点，对顶角有 对，邻补角有 对．

Answer 1

【答案】(1)1,3,画图见解析, 对顶角有6对，邻补角有12对;(2)1,6, 画图见解析, 对顶角有12对，邻补角有24对;(3)1, , n(n－1),2n(n－1).

【解析】试题分析：当直线同交于一点时，只有一个交点；当直线两两相交，且不过同一点时，交点个数最多；根据对顶角与邻补角的定义找出即可．

（1）三条直线相交，最少有1个交点，最多有3个交点，如图：

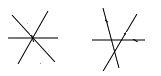
对顶角：6对，邻补角：12对；

（2）四条直线相交，最少有1个交点，最多有6个交点，如图：

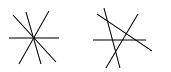
对顶角：12对，邻补角：24对；

（3）n条直线相交，最少有1个交点，最多有个交点，对顶角有n（n﹣1）对，邻补角有2n（n﹣1）对．

故答案为：（1）1，3；（2）1，6；（3）1， ，n（n﹣1），2n（n﹣1）．