Question

在△ABC中，AB=AC，CD⊥AB交AB于点D，将三角板MNP按图甲的位置摆放，使三角板的一条直角边MP与AC边在一条直线上，当另一条直角边MN恰好经过点B时，易证：BM=CD．

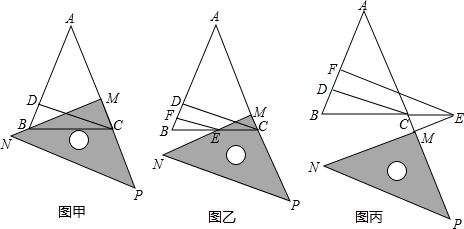
（1）当三角板沿AC方向平移到图乙的位置（一条直角边MP仍与AC边在同一直线上，另一条直角边MN交BC边于点E，过点E作EF⊥AB于点F）时，请你猜想线段EF、EM、CD之间的数量关系，并证明你的猜想；
（2）当三角板沿AC方向继续平移到图丙所示的位置（线段NM的延长线与BC的延长线交于点E）时，线段EF、EM、CD之间的又有怎样的数量关系？请写出你的猜想，不需证明．

Answer 1

分析：（1）首先构造直角三角形，进而利用全等三角形的判定得出△EWC≌△CME（AAS），即可得出EF、EM、CD之间的数量关系；
（2）首先构造直角三角形，进而利用全等三角形的判定得出△EWC≌△EMC，即可得出EF、EM、CD之间的数量关系．

解答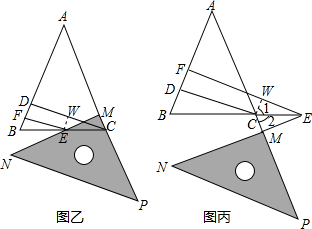：解：（1）EF+ME=CD，
理由：过点E作EW⊥CD于点W，
∵EF⊥AB，CD⊥AB，EW⊥CD，
∴四边形DFEW是矩形，
∴DW=EF，BD∥WE，
∴∠B=∠WEC，
∵AB=AC，
∴∠B=∠ACB，
∴∠ACB=∠WEC，
在△EWC和△CME中

∠EMC=∠CWE ∠WEC=∠MCE EC=EC

，
∴△EWC≌△CME（AAS），
∴WC=ME，
∴CD=DW+WC=EF+ME；

（2）EF=ME+CD，
理由：过点C作CW⊥EF于点W，
∵EF⊥AB，CD⊥AB，CW⊥EF，
∴四边形DFWC是矩形，
∴DC=WF，BA∥WC，
∴∠B=∠1，
∵AB=AC，
∴∠B=∠ACB，
∵∠ACB=∠2，
∴∠1=∠2，
在△EWC和△EMC中

∠EWC=∠EMC=90° ∠1=∠2 EC=EC

，
∴△EWC≌△EMC（AAS），
∴WE=ME，
∴EF=FW+WE=CD+ME．

点评：此题主要考查了全等三角形的判定与性质以及矩形的性质和等腰三角形的性质等知识，熟练利用相关性质得出对应角之间的关系是解题关键．