题目内容
如图,在梯形ABCD中,AD∥BC,点E为CD上一点,且DE=EC=BC.
(1)若∠B=90°,求证:∠AEC=3∠DAE;
(2)若tan∠DAE=
,AD=2,AE=5,求梯形ABCD的面积.

(1)若∠B=90°,求证:∠AEC=3∠DAE;
(2)若tan∠DAE=
| 4 |
| 3 |

(1)证明:延长AE交BC的延长线于F,连接BE,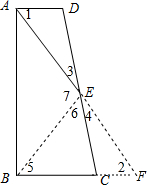
∵AD∥BC,
∴∠1=∠2,
在△ADE和△FCE中,
∵
∴△ADE≌△FCE,
∴AE=EF,
又∵△ABF为直角三角形,
∴BE=EF,
∴∠5=∠2=∠1,
∴∠7=2∠1,
又∵CE=BC,
∴∠5=∠6=∠1,
∴∠AEC=∠6+∠7=3∠1,
即∠AEC=3∠DAE.
(2)过D作DH⊥AE于H,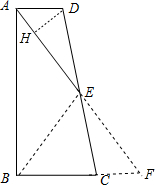
由(1)SABCD=S△ABF=2S△BEF,
∵在Rt△ADH中,tan∠DAH=
,
∴sin∠DAE=
=
,
即
=
,
∴DH=
,
∵tan∠DAE=
=
,
∴AH=
,
∴S△ADE=
×AE×DH=
×5×
=4,
∴S△ECF=4,
∵AE=5,AH=
,
∴HE=5-
=
,
在Rt△DHE中,由勾股定理得:DE=
,
即BC=DE=
,
∵CF=AD=2,
∴
=
,
∴S△BCE=
×4=2
,
∴S△EBF=2
+4,
∴S△ABF=2S△EBF=4
+8,
即S梯形ABCD=4
+8.

∵AD∥BC,
∴∠1=∠2,
在△ADE和△FCE中,
∵
|
∴△ADE≌△FCE,
∴AE=EF,
又∵△ABF为直角三角形,
∴BE=EF,
∴∠5=∠2=∠1,
∴∠7=2∠1,
又∵CE=BC,
∴∠5=∠6=∠1,
∴∠AEC=∠6+∠7=3∠1,
即∠AEC=3∠DAE.
(2)过D作DH⊥AE于H,

由(1)SABCD=S△ABF=2S△BEF,
∵在Rt△ADH中,tan∠DAH=
| 4 |
| 3 |
∴sin∠DAE=
| 4 |
| 5 |
| DH |
| AD |
即
| 4 |
| 5 |
| DH |
| 2 |
∴DH=
| 8 |
| 5 |
∵tan∠DAE=
| 4 |
| 3 |
| DH |
| AH |
∴AH=
| 6 |
| 5 |
∴S△ADE=
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| 5 |
∴S△ECF=4,
∵AE=5,AH=
| 6 |
| 5 |
∴HE=5-
| 6 |
| 5 |
| 19 |
| 5 |
在Rt△DHE中,由勾股定理得:DE=
| 17 |
即BC=DE=
| 17 |
∵CF=AD=2,
∴
| S△BCE |
| S△ECF |
| ||
| 2 |
∴S△BCE=
| ||
| 2 |
| 17 |
∴S△EBF=2
| 17 |
∴S△ABF=2S△EBF=4
| 17 |
即S梯形ABCD=4
| 17 |

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目


 点P、Q分别从A、C同时出发,设运动时间为t(s).
点P、Q分别从A、C同时出发,设运动时间为t(s).


 到达顶点时,另一点也随之停止运动,设运动时间为t(s),问t为何值时,
到达顶点时,另一点也随之停止运动,设运动时间为t(s),问t为何值时,