题目内容
【题目】填空:把下面的推理过程补充完整,并在括号内注明理由.
已知:如图,△ABC中,D、E分别为AB、AC的中点,过点C作CF//AB交DE的延长线于F.求证:AB=2CF.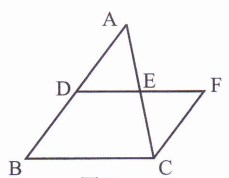
证明:∵CF//AB(已知),
∴∠ADE=∠F( ![]() ),
),
∵E为AC的中点(已知),
∴AE=CE(中点的定义).
在△ADE与△CFE中,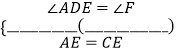
∴△ADE△CFE( ![]() )
)
∴AD=CF( ![]() )
)
∵D为AB的中点
∴AB=2AD(中点的定义)
∴AB=2CF(等量代换)
【答案】解:证明:∵ CF//AB(已知)
∴∠ADE=∠F( 两直线平行,内错角相等 )
∵E为AC的中点(已知)
∴AE=CE(中点的定义)
在△ADE与△CFE中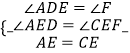 ( 对顶角相等 )
( 对顶角相等 )
∴△ADE≌△CFE( AAS )
∴AD=CF(全等三角形的对应边相等)
∵D为AB的中点
∴AB=2AD(中点的定义)
∴AB=2CF(等量代换)
【解析】证明题中每一步要求做到有理有据的,条理清晰;根据解题步骤给出的条件和结论,找它的“有关的定义和定理”填在空里即可.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目