题目内容
【题目】已知抛物线![]() =
=![]() (
(![]() ≠0)与
≠0)与![]() 轴交于AB两点,与
轴交于AB两点,与![]() 轴交于C点,其对称轴为
轴交于C点,其对称轴为![]() =1,且A(-1,0)C(0,2).
=1,且A(-1,0)C(0,2).
(1)直接写出该抛物线的解析式;
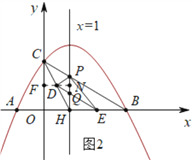
(2)P是对称轴上一点,△PAC的周长存在最大值还是最小值?请求出取得最值(最大值或最小值)时点P的坐标;
(3)设对称轴与![]() 轴交于点H,点D为线段CH上的一动点(不与点CH重合).点P是(2)中所求的点.过点D作DE∥PC交
轴交于点H,点D为线段CH上的一动点(不与点CH重合).点P是(2)中所求的点.过点D作DE∥PC交![]() 轴于点E.连接PDPE.若CD的长为
轴于点E.连接PDPE.若CD的长为![]() ,△PDE的面积为S,求S与
,△PDE的面积为S,求S与![]() 之间的函数关系式,试说明S是否存在最值,若存在,请求出最值,并写出S取得的最值及此时
之间的函数关系式,试说明S是否存在最值,若存在,请求出最值,并写出S取得的最值及此时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1) ![]() =-
=-![]() +
+![]() +2;(2) P(1,
+2;(2) P(1,![]() );(3)见解析.
);(3)见解析.
【解析】分析:
(1)由已知条件易得点B的坐标为(3,0),这样结合点A、C的坐标即可求得抛物线的解析式;
(2)由题意可知,AC长度是固定值,点A和点B关于直线x=1对称,由此可得连接BC交直线x=1于点P,此时△PAC的周长最小,求得直线BC的解析式,即可求得此时点P的坐标;
(3)如图2,画出符合题意的图形,过点D作DF⊥y轴于点F,交对称轴x=1于点N,在Rt△OCH中易得CH=![]() ,由Rt△CDF∽Rt△CHO,可将CF、OF和FD用含m的代数式表达出来,从而可表达出点D和点N的坐标,再用待定系数法求得用含m的代数式表达的DE的解析式,即可表达出点E的坐标和点Q的坐标,然后由S=S△PDE=S△PDQ+S△PEQ=即可得到S与m间的函数关系式,将所得解析式化简、配方即可得到所求答案.
,由Rt△CDF∽Rt△CHO,可将CF、OF和FD用含m的代数式表达出来,从而可表达出点D和点N的坐标,再用待定系数法求得用含m的代数式表达的DE的解析式,即可表达出点E的坐标和点Q的坐标,然后由S=S△PDE=S△PDQ+S△PEQ=即可得到S与m间的函数关系式,将所得解析式化简、配方即可得到所求答案.
详解:
(1)∵抛物线![]() =
=![]() (
(![]() ≠0)与
≠0)与![]() 轴交于AB两点,其对称轴为
轴交于AB两点,其对称轴为![]() =1,且A(-1,0),
=1,且A(-1,0),
∴点B的坐标为(3,0),
∴可设抛物线解析式为:![]() ,
,
∵抛物线和y轴交于点C(0,2),
∴![]() ,解得:
,解得:![]() ,
,
∴![]() ,即
,即![]() ;
;
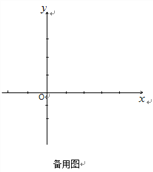
(2)△PAC的周长有最小值,连结ACBC,
∵AC的长度一定,
∴要使△PAC的周长最小,就是使PA+PC最小.
∵点A关于对称轴![]() =1的对称点是B点,
=1的对称点是B点,
∴BC与对称轴的交点即为所求的点P(如图2),
设直线BC的表达为![]() :
:![]() =
= ,则有
,则有
![]() ,解得
,解得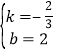 ,∴
,∴![]() :
:![]() =-
=-![]() +2,
+2,
把![]() =1代入,得
=1代入,得![]() =
=![]() ,
,
即点P的坐标为P(1,![]() ),
),
∴△PAC的周长取得最小值,取得最小值时点P的坐标为P(1,![]() );
);

(3)如图2,设DE对称轴x=1于点Q,
在Rt△COH中,由勾股定理得CH=![]() =
=![]() =
=![]() .
.
过点D作DF⊥![]() 轴于点F,交对称轴
轴于点F,交对称轴![]() =1于点N,
=1于点N,
∵Rt△CDF∽Rt△CHO,
∴![]() ,
,
∴CF=![]() =
=![]() =
=![]() ,OF=CO-CF=2-
,OF=CO-CF=2-![]() ;
;
同样: ![]() ,FD=
,FD=![]() =
=![]() =
=![]() ,
,
∴点D的坐标为D(![]() ,2-
,2-![]() ),
),
∴N(1,2-![]() ).
).
∵DE∥BC,
∴可设![]() (过点DE的直线):
(过点DE的直线):![]() =-
=-![]() +
+![]() ,
,
把D点坐标代入其中,得-![]()
![]() +
+![]() =2-
=2-![]() ,
,
解得![]() =2-
=2-![]() ,
,
∴![]() :
:![]() =-
=-![]() +2-
+2-![]() ,
,
点E的纵坐标为0,代入其中,解得![]() =3-
=3-![]() ,
,
∴E(3-![]() ,0).
,0).
∵点Q在对称轴![]() =1上,把
=1上,把![]() =1代入
=1代入![]() 中,解得
中,解得![]() =
=![]() -
-![]() ,
,
∴Q(1,![]() -
-![]() ).
).
PQ=![]() -(
-(![]() -
-![]() )=
)=![]() ,DN=1-
,DN=1-![]() ,
,
EH=3-![]() -1=2-
-1=2-![]() .
.
S=S△PDE=S△PDQ+S△PEQ=![]() PQ·DN+
PQ·DN+![]() PQ·EH
PQ·EH
=![]() PQ(DN+EH)=
PQ(DN+EH)=![]() ·
·![]() (1-
(1-![]() +2-
+2-![]() ),
),
化简得S=-![]() +
+![]() ,
,
可知S是关于![]() 的二次函数.
的二次函数.
S存在最大值.
配方可得:S=-![]() +
+![]() ,由此可得,S取得最大值为
,由此可得,S取得最大值为![]() ,
,
取得最大值时![]() 的值为:
的值为:![]() =
=![]() .
.

【题目】某市水果批发部门欲将 A 市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为 200 元/ 时.其它主要参考数据如下:
运输工具 | 途中平均速度(千米/ 时) | 运费(元/ 千米) | 装卸费用(元) |
火车 | 100 | 15 | 2000 |
汽车 | 80 | 20 | 900 |
运输过程中,火车因多次临时停车,全程在路上耽误 2 小时 45 分钟,火车的总支出费用与汽车的总支出费用相同,请问某市与本地的路程是多少千米?