Question

【题目】四边形ABCD是正方形，△ADF旋转一定角度后得到△ABE，如图所示，如果AF=4，AB=7，

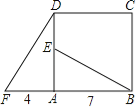
（1）指出旋转中心和旋转角度；

（2）求DE的长度；

（3）BE与DF的位置关系如何？

Answer 1

【答案】（1）旋转角度为90°或270°；（2）DE= 3；（3）BE与DF是垂直关系．

【解析】试题先根据正方形的性质得到：△AFD≌△AEB，从而得出等量关系AE=AF=4，∠EAF=90°，∠EBA=∠FDA，找到旋转中心和旋转角度．这些等量关系即可求出DE=AD﹣AE=7﹣4=3；BE⊥DF．

解：（1）根据正方形的性质可知：△AFD≌△AEB，即AE=AF=4，∠EAF=90°，∠EBA=∠FDA；

可得旋转中心为点A；旋转角度为90°或270°；

（2）DE=AD﹣AE=7﹣4=3；

（3）∵∠EAF=90°，∠EBA=∠FDA，

∴延长BE与DF相交于点G，则∠GDE+∠DEG=90°，

∴BE⊥DF，

即BE与DF是垂直关系．