题目内容
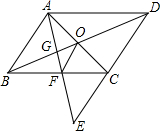 已知:如图,E为?ABCD中DC边的延长线上一点,且CE=DC,连接AE,分别交BC、BD于点F、G,连接AC交BD于O,连接OF,判断AB与OF的位置关系和大小关系,并证明你的结论.
已知:如图,E为?ABCD中DC边的延长线上一点,且CE=DC,连接AE,分别交BC、BD于点F、G,连接AC交BD于O,连接OF,判断AB与OF的位置关系和大小关系,并证明你的结论.
分析:本题可先证明△ABF≌△ECF,从而得出BF=CF,这样就得出了OF是△ABC的中位线,从而利用中位线定理即可得出线段OF与线段AB的关系.
解答:解:AB=2OF.
证明:∵四边形ABCD是平行四边形,
∴AB=CD,OA=OC.
∴∠BAF=∠CEF,∠ABF=∠ECF.
∵CE=DC,
在平行四边形ABCD中,CD=AB,
∴AB=CE.
∴在△ABF和△ECF中,
,
∴△ABF≌△ECF(ASA),
∴BF=CF.
∵OA=OC,
∴OF是△ABC的中位线,
∴AB=2OF,AB∥OF.
证明:∵四边形ABCD是平行四边形,
∴AB=CD,OA=OC.
∴∠BAF=∠CEF,∠ABF=∠ECF.
∵CE=DC,
在平行四边形ABCD中,CD=AB,
∴AB=CE.
∴在△ABF和△ECF中,
|
∴△ABF≌△ECF(ASA),
∴BF=CF.
∵OA=OC,
∴OF是△ABC的中位线,
∴AB=2OF,AB∥OF.
点评:此题主要考查了平行四边形的性质,全等三角形的性质与判定及三角形的中位线定理,综合的知识点比较多,解答本题的关键是判断出OF是△ABC的中位线.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
 点E.
点E.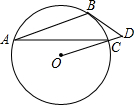 已知:如图,AB为⊙O的弦,过点O作AB的平行线,交⊙O于点C,直线OC上一点D满足∠D=∠ACB.
已知:如图,AB为⊙O的弦,过点O作AB的平行线,交⊙O于点C,直线OC上一点D满足∠D=∠ACB.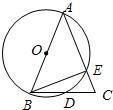 已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45度.给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧AE是劣弧DE的2倍;⑤AE=BC.其中正确结论的序号是( )
已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45度.给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧AE是劣弧DE的2倍;⑤AE=BC.其中正确结论的序号是( ) 已知:如图,BD为ABCD的对角线,O为BD的中点,EF⊥BD于点O,与AD、BC分别交于点E、F.求证:DE=DF.
已知:如图,BD为ABCD的对角线,O为BD的中点,EF⊥BD于点O,与AD、BC分别交于点E、F.求证:DE=DF.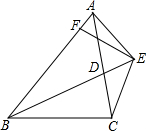 已知:如图,BD为∠ABC的角平分线,且BD=BC,E为BD的延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①∠ABE=∠ACE;②∠BCE+∠BCD=180°;③AE=EC;④BE+BD=2BF,其中正确的是( )
已知:如图,BD为∠ABC的角平分线,且BD=BC,E为BD的延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①∠ABE=∠ACE;②∠BCE+∠BCD=180°;③AE=EC;④BE+BD=2BF,其中正确的是( )