题目内容
(12分)某冰箱厂为响应国家“家电下乡”号召,计划生产 、
、 两种型号的冰箱100台.经预算,两种冰箱全部售出后,可获得利润不低于 4.75万元,不高于4.8万元,两种型号的冰箱生产成本和售价如下表:
两种型号的冰箱100台.经预算,两种冰箱全部售出后,可获得利润不低于 4.75万元,不高于4.8万元,两种型号的冰箱生产成本和售价如下表:
⑴冰箱厂有哪几种生产方案?
⑵该冰箱厂按哪种方案生产,才能使投入成本最少?“家电下乡”后农民买家电(冰箱、彩电、洗衣机)可享受售价13%的政府补贴,那么在这种方案下政府需补贴给农民多少元?
⑶若按⑵中的方案生产,冰箱厂计划将获得的全部利润购买三种物品:体育器材、实验设备、办公用品支援某希望小学.其中体育器材至多买4套,体育器材每套6000元,实验设备每套3000元,办公用品每套1800元,把钱全部用尽且三种物品都购买的情况下,请你直接写出实验设备的买法共有多少种.
 、
、 两种型号的冰箱100台.经预算,两种冰箱全部售出后,可获得利润不低于 4.75万元,不高于4.8万元,两种型号的冰箱生产成本和售价如下表:
两种型号的冰箱100台.经预算,两种冰箱全部售出后,可获得利润不低于 4.75万元,不高于4.8万元,两种型号的冰箱生产成本和售价如下表:| 型号 | A型 | B型 |
| 成本(元/台) | 2200 | 2600 |
| 售价(元/台) | 2800 | 3000 |
⑵该冰箱厂按哪种方案生产,才能使投入成本最少?“家电下乡”后农民买家电(冰箱、彩电、洗衣机)可享受售价13%的政府补贴,那么在这种方案下政府需补贴给农民多少元?
⑶若按⑵中的方案生产,冰箱厂计划将获得的全部利润购买三种物品:体育器材、实验设备、办公用品支援某希望小学.其中体育器材至多买4套,体育器材每套6000元,实验设备每套3000元,办公用品每套1800元,把钱全部用尽且三种物品都购买的情况下,请你直接写出实验设备的买法共有多少种.
①  ,生产方案:A型38台B型62台,A型39台B型61台,A型40台B型60台 ② A型40台B型60台 37960 ③ 7种方案
,生产方案:A型38台B型62台,A型39台B型61台,A型40台B型60台 ② A型40台B型60台 37960 ③ 7种方案
 ,生产方案:A型38台B型62台,A型39台B型61台,A型40台B型60台 ② A型40台B型60台 37960 ③ 7种方案
,生产方案:A型38台B型62台,A型39台B型61台,A型40台B型60台 ② A型40台B型60台 37960 ③ 7种方案试题分析:(1)设A型号售x台,B型号售y台,上述题目得出两个条件:x+y=100;
47500≤(2800-2200)x+(3000-2600)y≤48000;以x来推导得到
 ;所以x得到了38,39,40三种方案。
;所以x得到了38,39,40三种方案。(2)设总成本为z,成本函数为:
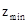 =2200x+2600y,结合上(1)的条件x+y=100,得到函数
=2200x+2600y,结合上(1)的条件x+y=100,得到函数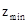 =-400x+2600.根据一次函数性质当k小于0,y随x的增大而减小,所以当x取40时,z值取最小。
=-400x+2600.根据一次函数性质当k小于0,y随x的增大而减小,所以当x取40时,z值取最小。根据x+y=100和13%(2800x+3000y),得出37960。
(3)根据上述问题,得到的利润为48000,设体育器材x套,实验设备y套,办公用品z套,
假设函数6000x+3000y+1800z=48000,而1≤x≤4,得到24000≤3000y+1800z≤42000,假设x=1时
3000y +1800z=24000。可得一次函数解析式
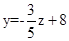 ,当x=0时,y=8.则能取的整数为1到8之间8个数。以描点法排除去对应z不是整数的情况。可以得到2个点符合题设。再以此分别求出x=2,x=3,x=4情况下,符合的y和z的一次函数及取值。一共7种方案。
,当x=0时,y=8.则能取的整数为1到8之间8个数。以描点法排除去对应z不是整数的情况。可以得到2个点符合题设。再以此分别求出x=2,x=3,x=4情况下,符合的y和z的一次函数及取值。一共7种方案。点评:本题难度较大。主要考查学生对解决实际问题使用方程组,消元法,一次函数等方面的综合运用。这类题含3个未知数,一般解题关键是先设定其中一个未知数的值,求出另外两个未知数的函数解析式来分析。

练习册系列答案
相关题目


 ,两车之间的距离为
,两车之间的距离为 ,图中的折线表示
,图中的折线表示 与
与 之间的函数关系.
之间的函数关系.
 的实际意义;
的实际意义; (千米)与时间
(千米)与时间 (小时)的函数图象如图所示.
(小时)的函数图象如图所示.
 .小王与小张在途中共相遇几次?请你计算第一次相遇的时间.
.小王与小张在途中共相遇几次?请你计算第一次相遇的时间.




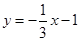 的图象上的点是( )
的图象上的点是( )
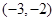


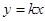 与
与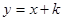 交点的横坐标是2,则交点坐标是( ).
交点的横坐标是2,则交点坐标是( ).