题目内容
【题目】如图,在ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC. 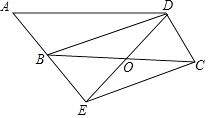
(1)求证:四边形BECD是平行四边形;
(2)若∠A=50°,则当∠BOD=°时,四边形BECD是矩形.
【答案】
(1)证明:∵四边形ABCD为平行四边形,
∴AB∥DC,AB=CD,
∴∠OEB=∠ODC,
又∵O为BC的中点,
∴BO=CO,
在△BOE和△COD中, 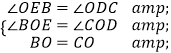 ,
,
∴△BOE≌△COD(AAS);
∴OE=OD,
∴四边形BECD是平行四边形;
(2)100
【解析】(2)解:若∠A=50°,则当∠BOD=100°时,四边形BECD是矩形.理由如下: ∵四边形ABCD是平行四边形,
∴∠BCD=∠A=50°,
∵∠BOD=∠BCD+∠ODC,
∴∠ODC=100°﹣50°=50°=∠BCD,
∴OC=OD,
∵BO=CO,OD=OE,
∴DE=BC,
∵四边形BECD是平行四边形,
∴四边形BECD是矩形;
所以答案是:100.
【考点精析】认真审题,首先需要了解平行四边形的判定与性质(若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积),还要掌握矩形的判定方法(有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形)的相关知识才是答题的关键.

练习册系列答案
相关题目