题目内容
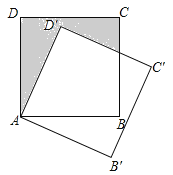
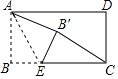
【题目】如图，点E是矩形纸片的边BC上的一动点，沿直线AE折叠纸片，点B落在了点B′位置，连结CB′．已知AB=3，BC=6，则当线段CB′最小时BE的长为______.
【答案】
【解析】
如图，连接AC．当A、B′、C共线时，CB′的值最小．设BE=EB′=x，在Rt△CBE′中，EC=6-x，CB′=3
-3，EB′=x，利用勾股定理构建方程即可解决问题；
解：如图，连接AC．
∵四边形ABCD是矩形，
∴∠B=90°，
∴AC=
=
=
,
∵CB′≥AC-AB′，
∴当A、B′、C共线时，CB′的值最小．
设BE=EB′=x，
在Rt△CBE′中，EC=6-x，CB′=3 -3，EB′=x，
∴x2+（3-3）2=（6-x）2，
∴x=
,
∴BE=,
故答案为.
练习册系列答案
阅读快车系列答案
相关题目
