题目内容
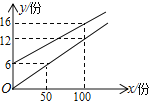
【题目】如图,直线![]() 的表达式为
的表达式为![]() ,且
,且![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过点
经过点![]() ,
,![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() .
.
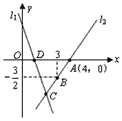
(1)求点![]() 的坐标;
的坐标;
(2)求直线![]() 的表达式;
的表达式;
(3)在直线![]() 上有异于点
上有异于点![]() 的另一点
的另一点![]() ,使得
,使得![]() 与
与![]() 的面积相等,请直接写出点
的面积相等,请直接写出点![]() ,点
,点![]() 的坐标.
的坐标.
【答案】(1)点![]() 的坐标为
的坐标为![]() ;(2)直线
;(2)直线![]() 的表达式为
的表达式为![]() ;(3)
;(3)![]() 的坐标为
的坐标为![]() 点
点![]() 的坐标为
的坐标为![]() .
.
【解析】
已知l1的解析式,令y=0求出x的值即可得到点D的坐标;
设l2的解析式为y=kx+b,利用待定系数法即可求出函数的表达式;
(3),联立两个函数解析式,求出交点C的坐标, △ADP与△ADC底边都是AD,面积相等所以高相等,可根据对称解答.
解:(1)由y=-3x+3,令y=0,得-3x+3=0,
∴x=1,
∴D(1,0);
(2)设直线l2的解析表达式为y=kx+b,
由图象知:x=4,y=0;x=3,y=![]() ,
,
∴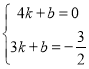
∴k=![]() ,b=-6,
,b=-6,
∴直线l2的解析表达式为y=![]() x-6;
x-6;
(3)由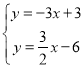
解得x=2,y=-3,
∴C(2,-3).
因为![]() 与
与![]() 的面积相等,
的面积相等,
P与C必然根据点A对称,
可得P(6,3).

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
【题目】新华文具用品店最近购进了一批钢笔,进价为每支6元,为了合理定价,在销售前4天试行机动价格,卖出时每支以10元为标准,超过10元的部分记为正,不足10元的部分记为负。文具店记录了这四天该钢笔的售价情况和售出情况,如下表所示:
第1天 | 第2天 | 第3天 | 第4天 | |
每支价格相对标准价格(元) | +1 | 0 | -1 | -2 |
售出支数(支) | 12 | 15 | 32 | 33 |
(1)填空:这四天中赚钱最多的是第______天,这天赚了______元钱;
(2)求新华文具用品店这四天出售这种钢笔一共赚了多少钱;
(3)新华文具用品店准备用这四天赚的钱全部购进这种钢笔,进价仍为每支6元为了促销这种钢笔,每只钢笔的售价在10元的基础上打九折,本次购进的这种钢笔全部售出后共赚了多少钱?