题目内容
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中记载了一个“折竹抵地”问题:“今有竹高二丈,末折抵地,去本六尺,问折者高几何?”
译文:“有一根竹子,原高二丈(1丈=10尺),现被风折断,竹梢触地面处与竹根的距离为6尺,问折断处离地面的高度为多少尺?”
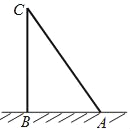
如图,我们用点A,B,C分别表示竹梢,竹根和折断处,设折断处离地面的高度BC=x尺,则可列方程为_____.
【答案】x2+62=(20﹣x)2.
【解析】
竹子折断后刚好构成一直角三角形,设竹子折断处离地面x尺,则斜边为(20﹣x)尺,利用勾股定理解题即可.
设竹子折断处离地面x尺,则斜边为(20﹣x)尺,根据勾股定理得:x2+62=(20﹣x)2.
故答案为:x2+62=(20﹣x)2.

练习册系列答案
相关题目